(1)由等比数列递增的性质得其首项为1,公比为4,可得到通项公式;(2)先由数列的前两项满足等式,求出
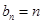
;再写出
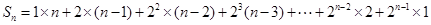
,错位相减求出
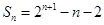
。即证出存在数列{b
n},结论成立
(1)因为{a
n}是递增的等比数列,所以数列{a
n}的公比是正数,
又{a
1,a
3,a
5}
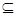
{-10,-6,-2,0,1,3,4,16},所以a
1=1,a
3=4,a
5=16,
从而q
2=
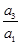
=4,q=2,a
n=a
1q
n-1=2
n-1,所以数列{a
n}的通项公式为a
n=2
n-1,
(2)假设存在满足条件的等差数列{b
n},其公差为d.则当n=1时,a
1b
1=1,
又∵a
1=1,∴b
1=1;
当n=2时,a
1b
2+a
2b
1=4,b
2+2b
1=4,b
2=2.
则d=b
2-b
1=1,∴b
n=b
1+(n-1)d=1+(n-1)×1=n.
以下证明当b
n=n时,a
1b
n+a
2b
n-1+…+a
n-1b
2+a
nb
1=2
n+1-n-2对一切n∈N
*都成立.
设S
n=a
1b
n+a
2b
n-1+…+a
n-1b
2+a
nb
1,
即S
n=1×n+2×(n-1)+2
2×(n-2)+2
3×(n-3)+…+2
n-2×2+2
n-1×1, ①
2S
n=2×n+2
2×(n-1)+2
3×(n-2)+…+2
n-1×2+2
n×1, ②
②-①得S
n=-n+2+2
2+2
3+…+2
n-1+2
n=-n+

=2
n+1-n-2,
所以存在等差数列{b
n},b
n=n,使得a
1b
n+a
2b
n-1+…+a
n-1b
2+a
nb
1=2
n+1-n-2对一切n∈N
*都成立.

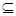 {-10,-6,-2,0,1,3,4,16}.
{-10,-6,-2,0,1,3,4,16}.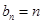 ;再写出
;再写出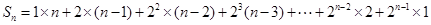 ,错位相减求出
,错位相减求出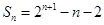 。即证出存在数列{bn},结论成立
。即证出存在数列{bn},结论成立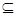 {-10,-6,-2,0,1,3,4,16},所以a1=1,a3=4,a5=16,
{-10,-6,-2,0,1,3,4,16},所以a1=1,a3=4,a5=16,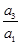 =4,q=2,an=a1qn-1=2n-1,所以数列{an}的通项公式为an=2n-1,
=4,q=2,an=a1qn-1=2n-1,所以数列{an}的通项公式为an=2n-1, =2n+1-n-2,
=2n+1-n-2,
