
【题目】如图,正四面体ABCD中,E、F分别是棱BC和AD的中点,则直线AE和CF所成的角的余弦值为( ) 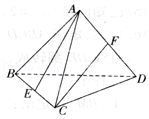
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:连接BF、EF, ∵正四面体ABCD中,E、F分别是棱BC和AD的中点,
∴BF⊥AD,CF⊥AD,
又BF∩CF=F,∴AD⊥面BCF,
∴AE在平面BCF上的射影为EF,
设异面直线AE和CF所成的角为θ,正四面体棱长为1,
则 ![]() ,
, ![]() .
.
∵cosθ=cos∠AEFcos∠EFC,
∴cosθ= ![]() =
= ![]() .
.
故直线AE和CF所成的角的余弦值为 ![]() .
.
故选:B.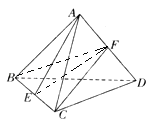
【考点精析】关于本题考查的异面直线及其所成的角,需要了解异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系才能得出正确答案.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:函数f(x)=lg(ax2﹣ax+1)的定义域是R;命题 ![]() 在第一象限为增函数,若“p∧q”为假,“p∨q”为真,求a的取值范围.
在第一象限为增函数,若“p∧q”为假,“p∨q”为真,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣alnx﹣a. (Ⅰ)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)证明:对于a∈(0,e),f(x)在区间 ![]() 上有极小值,且极小值大于0.
上有极小值,且极小值大于0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,∠ACB=90°,AC=BC=1,AA1=2,D是棱AA1的中点. 
(Ⅰ)求证:B1C1∥平面BCD;
(Ⅱ)求三棱锥B﹣C1CD的体积;
(Ⅲ)在线段BD上是否存在点Q,使得CQ⊥BC1?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点. 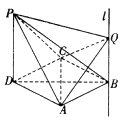
(1)求证:QP⊥AC;
(2)当二面角Q﹣AC﹣P的大小为120°时,求QB的长;
(3)在(2)的条件下,求三棱锥Q﹣ACP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校有2500名学生,其中高一1000人,高二900人,高三600人,为了了解学生的身体健康状况,采用分层抽样的方法,若从本校学生中抽取100人,从高一和高三抽取样本数分别为a,b,且直线ax+by+8=0与以A(1,﹣1)为圆心的圆交于B,C两点,且∠BAC=120°,则圆C的方程为( )
A.(x﹣1)2+(y+1)2=1
B.(x﹣1)2+(y+1)2=2
C.(x﹣1)2+(y+1)2= ![]()
D.(x﹣1)2+(y+1)2= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(1﹣2a)x﹣lnx(a∈R).
(1)求函数f(x)在区间[1,2]上的最大值;
(2)若A(x1 , y1),B(x2 , y2),C(x0 , y0)是函数f(x)图象上不同的三点,且x0= ![]() ,试判断f′(x0)与
,试判断f′(x0)与 ![]() 之间的大小关系,并证明.
之间的大小关系,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题,松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a=10,b=4,则输出的n=( ) 
A.4
B.5
C.6
D.7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com