练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     设f′(x)是函数f(x)的导数，y＝f′(x)的图像如图所示，则y＝f(x)的图像最有可能是(　　)B


    B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    在中，角A、B、C的对边分别为，已知向量且满足，（1）求角A的大小；

    （2）若试判断的形状。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


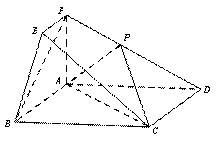
    在如图所示的几何体中，四边形ABCD为矩形，平面ABEF⊥平面ABCD， EF // AB，

    ∠BAF=90º， AD= 2，AB=AF=2EF =1，点P在棱DF上．                         

    （Ⅰ）若P是DF的中点

    (ⅰ) 求证：BF // 平面ACP

    (ⅱ) 求异面直线BE与CP所成角的余弦值

    （Ⅱ）若二面角D-AP-C的余弦值为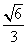，求PF的长度．

                                   

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    求值 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数有（    ）

    A．极大值，极小值            B．极大值，极小值

    C．极大值，无极小值              D．极小值，无极大值

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    曲线y＝x3－2x＋4在点(1,3)处的切线方程       

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)=lnx-ax2-2x,

    (1)若函数f(x)在x=2处取得极值,求实数a的值.

    (2)若函数f(x)在定义域内单调递增,求实数a的取值范围.

    (3)当a=-时,关于x的方程f(x)=-x+b在[1,4]上恰有两个不相等的实数根,求实数b的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设f(x)是定义在R上的增函数,且对于任意的x都有f(-x)+f(x)=0恒成立.如果实数m、n满足不等式f(m2-6m+21)+f(n2-8n)<0,那么m2+n2的取值范围是___________．

    ？
     

                                

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知直线l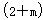：x＋y＋4－3m＝0.

    (1) 求证：不论m为何实数，直线l恒过一定点M；

    (2) 过定点M作一条直线l1，使夹在两坐标轴之间的线段被M点平分，求直线l1的方程．

    查看答案和解析>>

    同步练习册答案