
已知函数f(x)=lnx- ax2-2x,
ax2-2x,
(1)若函数f(x)在x=2处取得极值,求实数a的值.
(2)若函数f(x)在定义域内单调递增,求实数a的取值范围.
(3)当a=- 时,关于x的方程f(x)=-
时,关于x的方程f(x)=- x+b在[1,4]上恰有两个不相等的实数根,求实数b的取值范围.
x+b在[1,4]上恰有两个不相等的实数根,求实数b的取值范围.
【解析】(1)由题意,得f′(x)=-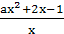 (x>0),
(x>0),
因为x=2时,函数f(x)取得极值,所以f′(2)=0,解得a=- ,经检验,符合题意.
,经检验,符合题意.
(2)函数f(x)的定义域为(0,+∞),依题意,f′(x)≥0在x>0时恒成立,即ax2+2x-1≤0在x>0时恒成立,则a≤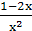 =
=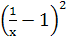 -1在x>0时恒成立,
-1在x>0时恒成立,
即a≤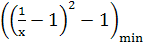 (x>0),
(x>0),
当x=1时,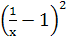 -1取最小值-1,所以a的取值范围是(-∞,-1].
-1取最小值-1,所以a的取值范围是(-∞,-1].
(3)当a=- 时,f(x)=-
时,f(x)=- x+b,即
x+b,即 x2-
x2- x+lnx-b=0.
x+lnx-b=0.
设g(x)= x2-
x2- x+lnx-b(x>0),则g′(x)=
x+lnx-b(x>0),则g′(x)=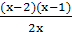 ,
,
当x变化时,g′(x),g(x)的变化情况如下表
| x | (0,1) | 1 | (1,2) | 2 | (2,4) |
| g′(x) | + | 0 | - | 0 | + |
| g(x) | ↗ | 极大 | ↘ | 极小 | ↗ |
所以g(x)极小值=g(2)=ln2-b-2,g(x)极大值=g(1)=-b- ,
,
又g(4)=2ln2-b-2,
因为方程g(x)=0在[1,4]上恰有两个不相等的实数根,
则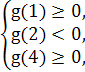 解得ln2-2<b≤-
解得ln2-2<b≤- ,
,
所以实数b的取值范围是(ln2-2,- ).
).


科目:高中数学 来源: 题型:
设直线x+ky-1=0被圆O:x2+y2=2所截弦的中点的轨迹为M,则曲线M与直线x-y-1=0的位置关系是( )
A.相离 B.相切 C.相交 D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线l:kx-y+1+2k=0.
(1) 求证:直线l过定点;
(2) 若直线l交x轴负半轴于点A,交y正半轴于点B,△AOB的面积为S,试求S的最小值并求出此时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com