
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, 在
在 上,
上,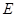 在
在 上.
上.
(1)设 ,求用
,求用 表示
表示 的函数关系式;
的函数关系式;
(2)如果 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短, 的位置应在哪里?如果
的位置应在哪里?如果 是参观线路,则希望它最长,
是参观线路,则希望它最长, 的位置又应在哪里?请说明理由.
的位置又应在哪里?请说明理由.
(1) =
=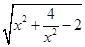 (1≤
(1≤ ≤2);(2)
≤2);(2) 为
为 中线或
中线或 中线时,
中线时, 最长.
最长.
解析试题分析:(1)在△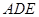 中,
中,
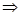
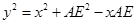 ,① 2分
,① 2分
又S△ADE= S△ABC=
S△ABC=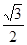 =
=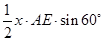
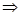
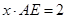 .② 3分
.② 3分
②代入①得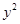 =
=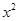 +
+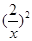 -2(
-2( >0), ∴
>0), ∴ =
=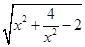 (1≤
(1≤ ≤2) 4分.
≤2) 4分.
(2)如果 是水管y=
是水管y=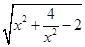 ≥
≥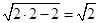 ,
,
当且仅当x2=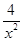 ,即x=
,即x=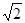 时“=”成立,故
时“=”成立,故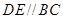 ,且
,且 =
=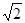 . 8分
. 8分
如果 是参观线路,记
是参观线路,记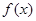 =
= 2+
2+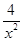 ,可知函数在[1,
,可知函数在[1,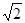 ]上递减,
]上递减,
在[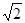 ,2]上递增,故
,2]上递增,故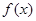 max=
max=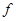 (1)=
(1)=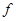 (2)=5. ∴
(2)=5. ∴ max=
max=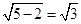 .
.
即 为
为 中线或
中线或 中线时,
中线时, 最长. 13分
最长. 13分
考点:本题主要考查函数模型,均值定理的应用。
点评:中档题,作为函数的应用问题,要遵循“审清题意,设出变量,列出等式,解答问题,作出结论”等步骤。求函数最值时,或利用导数,或利用均值定理,应根据题目特点,灵活选择方法。


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:解答题
某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车将会增加一辆。租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 .
.
(1)若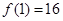 ,函数
,函数 是R上的奇函数,当
是R上的奇函数,当 时
时 ,
,
(i)求实数 与
与 的值;
的值;
(ii)当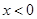 时,求
时,求 的解析式;
的解析式;
(2)若方程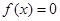 的两根中,一根属于区间
的两根中,一根属于区间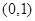 ,另一根属于区间
,另一根属于区间 ,求实数
,求实数 的
的
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
将边长为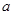 的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少?
的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com