
已知二次函数 ,满足
,满足 ,且方程
,且方程 有两个相等的实根.
有两个相等的实根.
(1)求函数 的解析式;
的解析式;
(2)当
 时,求函数
时,求函数 的最小值
的最小值 的表达式.
的表达式.
科目:高中数学 来源: 题型:解答题
运货卡车以每小时 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米
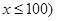 (单位:千米/小时).假设汽油的价格是每升6元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升6元,而汽车每小时耗油 升,司机的工资是每小时30元.
升,司机的工资是每小时30元.
(1)求这次行车总费用 关于
关于 的表达式;
的表达式;
(2)当 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, 在
在 上,
上,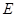 在
在 上.
上.
(1)设 ,求用
,求用 表示
表示 的函数关系式;
的函数关系式;
(2)如果 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短, 的位置应在哪里?如果
的位置应在哪里?如果 是参观线路,则希望它最长,
是参观线路,则希望它最长, 的位置又应在哪里?请说明理由.
的位置又应在哪里?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
2013年,首都北京经历了59年来雾霾天气最多的一个月。经气象局统计,北京市从1月1日至1月30日这30天里有26天出现雾霾天气。《环境空气质量指数(AQI)技术规定(试行)》将空气质量指数分为六级:其中,中度污染(四级),指数为151—200;重度污染(五级),指数为201—300;严重污染(六级),指数大于300. 下面表1是该观测点记录的4天里,AQI指数 与当天的空气水平可见度
与当天的空气水平可见度 (千米)的情况,表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数统计结果,
(千米)的情况,表2是某气象观测点记录的北京1月1日到1月30日AQI指数频数统计结果,
表1:AQI指数 与当天的空气水平可见度
与当天的空气水平可见度 (千米)情况
(千米)情况
AQI指数 |  |  |  |  |
空气可见度 (千米) (千米) |  |  |  |  |
| AQI指数 |  |  |  |  |  |
| 频数 | 3 | 6 | 12 | 6 | 3 |
 ,根据表1的数据,求出
,根据表1的数据,求出 关于
关于 的线性回归方程;
的线性回归方程;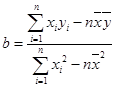 ,
, )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某企业在第1年初购买一台价值为120万元的设备M,M的价值在使用过程中逐年减少.从第2年到第6年,每年初M的价值比上年初减少10万元;从第7年开始,每年初M的价值为上年初的75%.
(1)求第n年初M的价值an的表达式;
(2)求数列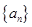 的前n项和
的前n项和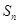
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产1百件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为5百件,产品销售数量为t(百件)时,销售所得的收入为( )万元。
)万元。
(1)该公司这种产品的年生产量为 百件,生产并销售这种产品得到的利润为当年产量
百件,生产并销售这种产品得到的利润为当年产量 的函数
的函数 ,求
,求 ;
;
(2)当该公司的年产量为多大时当年所获得的利润最大。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某房地产开发商投资81万元建一座写字楼,第一年维修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元。(1)n年利润是多少?第几年该楼年平均利润最大?最大是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,在
,在 时取得极值.
时取得极值.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(Ⅲ)若 ,是否存在实数b,使得方程
,是否存在实数b,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com