
某房地产开发商投资81万元建一座写字楼,第一年维修费为1万元,以后每年增加2万元,把写字楼出租,每年收入租金30万元。(1)n年利润是多少?第几年该楼年平均利润最大?最大是多少?
解析试题分析:(1)设第n年获取利润为y万元,n年共收入租金30n万元,付出装修费构成一个以1为首项, 2为公差的等差数列,共 n+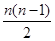 ×2=n2,
×2=n2,
因此利润y=30n-(81+n2),令y>0,解得:3<n<27,
所以从第4年开始获取纯利润.
(2)纯利润y=30n-(81+n2)=-(n-15)2+144,
所以15年后共获利润:144+10=154(万元)。
年平均利润W=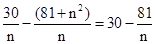 -n≤30-2
-n≤30-2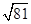 =12,(当且仅当
=12,(当且仅当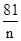 =n,即n=9时取等号)所以第9年获平均利润最大为12×9+46=154(万元)。
=n,即n=9时取等号)所以第9年获平均利润最大为12×9+46=154(万元)。
考点:本题主要考查函数模型,均值定理的应用。
点评:中档题,作为应用题,该题的综合性较强,解答过程中,要认真审题,特别是注意理解“利润”与“平均利润”的区别。应用均值定理,要注意“一正,二定,三相等”。


科目:高中数学 来源: 题型:解答题
某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车将会增加一辆。租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一边长为 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。
(1)试把方盒的容积 表示为
表示为 的函数;
的函数;
(2) 多大时,方盒的容积
多大时,方盒的容积 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
二次函数 的图像顶点为
的图像顶点为 ,且图像在x轴上截得线段长为8
,且图像在x轴上截得线段长为8
(1)求函数 的解析式;
的解析式;
(2)令
①若函数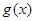 在
在 上是单调增函数,求实数
上是单调增函数,求实数 的取值范围;
的取值范围;
②求函数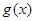 在
在 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用 平均建筑费用
平均建筑费用 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
将边长为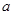 的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少?
的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一家报刊推销员从报社买进报纸的价格是每份0.20元,卖出的价格是每份0.30元,卖不完的还可以以每份0.08元的价格退回报社.在一个月(以30天计算)有20天每天可卖出400份,其余10天只能卖250份,但每天从报社买进报纸的份数都相同,问应该从报社买多少份才能使每月所获得的利润最大?并计算每月最多能赚多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com