
某公司生产一种产品,每年需投入固定成本0.5万元,此外每生产1百件这样的产品,还需增加投入0.25万元,经市场调查知这种产品年需求量为5百件,产品销售数量为t(百件)时,销售所得的收入为( )万元。
)万元。
(1)该公司这种产品的年生产量为 百件,生产并销售这种产品得到的利润为当年产量
百件,生产并销售这种产品得到的利润为当年产量 的函数
的函数 ,求
,求 ;
;
(2)当该公司的年产量为多大时当年所获得的利润最大。
 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:解答题
作为绍兴市2013年5.1劳动节系列活动之一的花卉展在镜湖湿地公园举行.现有一占地1800平方米的矩形地块,中间三个矩形设计为花圃(如图),种植有不同品种的观赏花卉,周围则均是宽为1米的赏花小径,设花圃占地面积为 平方米,矩形一边的长为
平方米,矩形一边的长为 米(如图所示)
米(如图所示)
(1)试将 表示为
表示为 的函数;
的函数;
(2)问应该如何设计矩形地块的边长,使花圃占地面积 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数 ,
, 是定义域为R上的奇函数.
是定义域为R上的奇函数.
(1)求 的值,并证明当
的值,并证明当 时,函数
时,函数 是R上的增函数;
是R上的增函数;
(2)已知 ,函数
,函数 ,
, ,求
,求 的值域;
的值域;
(3)若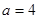 ,试问是否存在正整数
,试问是否存在正整数 ,使得
,使得 对
对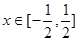 恒成立?若存在,请求出所有的正整数
恒成立?若存在,请求出所有的正整数 ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一边长为 的正方形铁片,铁片的四角截去四个边长均为
的正方形铁片,铁片的四角截去四个边长均为 的小正方形,然后做成一个无盖方盒。
的小正方形,然后做成一个无盖方盒。
(1)试把方盒的容积 表示为
表示为 的函数;
的函数;
(2) 多大时,方盒的容积
多大时,方盒的容积 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房.经测算,如果将楼房建为 层,则每平方米的平均建筑费用为
层,则每平方米的平均建筑费用为 (单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(单位:元).为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用 平均建筑费用
平均建筑费用 平均购地费用,平均购地费用
平均购地费用,平均购地费用 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在边长为60cm的正方形铁皮的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底边长为多少时,箱子容积最大?最大容积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com