
思路解析:本题可以根据圆的性质结合图形进行分析,这里牵涉到角的运算,所以可把圆的方程转化为参数方程进行运算.
解:如右图所示,利用同弧所对圆心角与圆周角的关系,可知∠BOC=120°,B、C两点中,只要一个确定,另一个也确定,为了便于解题,引入圆的参数方程![]() (θ为参数).
(θ为参数).
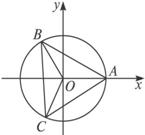
于是,设G(x,y),而点B的坐标记为(rcosθ,rsinθ),则点C的坐标为(rcos(120°+θ),rsin(120°+θ)).
从A、B、C三点互不重合得0°<θ<240°,利用重心坐标公式有
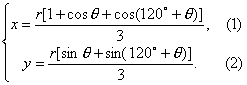
由式①,得3x-r=r[cosθ+cos(120°+θ)],即3x-r=rcos(60°+θ). ③
由式②,得3y=r[sinθ+sin(120°+θ)],即3y=rsin(60°+θ). ④
由③④平方相加可得(x-![]() )2+y2=(
)2+y2=(![]() )2.
)2.
由于0°<θ<240°,
所以0≤x=![]() <
<![]() ,
,
即△ABC的重心G的轨迹方程是(x-![]() )2+y2=(
)2+y2=(![]() )2,x∈[0,
)2,x∈[0,![]() ),
),
轨迹是一段圆弧.


科目:高中数学 来源: 题型:
| A、锐角三角形 | B、直角三角形 | C、钝角三角形 | D、以上情况都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:
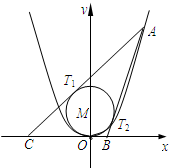 已知A是抛物线y=
已知A是抛物线y=| 1 |
| 4 |
| 1 |
| m |
| 1 |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com