
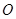 的半径是
的半径是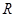 , 它的内接三角形
, 它的内接三角形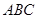 中, 有
中, 有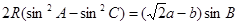 成立,求角
成立,求角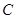 的大小及三角形面积
的大小及三角形面积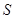 的最大值.
的最大值. 科目:高中数学 来源:不详 题型:解答题
 的方向,30 min后航行到B处,在B处看灯塔在船的北偏东
的方向,30 min后航行到B处,在B处看灯塔在船的北偏东 的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗?
的方向,已知距离此灯塔6.5n mile以外的海区为航行安全区域,这艘船可以继续沿正北方向航行吗? ="0.9063," sin20
="0.9063," sin20 =0.3420
=0.3420
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.
,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
,查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com