考点:利用导数求闭区间上函数的最值
专题:计算题,导数的综合应用
分析:由题意,令f(x)=
-
,从而求导f′(x)=
-
=
| xln2x-(x-1)2 |
| (x-1)2x(lnx)2 |
;再令g(x)=xln
2x-(x-1)
2并求导g′(x)=ln
2x+2lnx-2(x-1);g″(x)=
;再令h(x)=2lnx-2x+2并求导h′(x)=
-2;从而由导数的正负确定函数的单调性;再求
(
-
)=
=
=
=
;从而求a最小值.
解答:
解:由题意,令f(x)=
-
,
f′(x)=
-
=
| xln2x-(x-1)2 |
| (x-1)2x(lnx)2 |
;
令g(x)=xln
2x-(x-1)
2,
g′(x)=ln
2x+2lnx-2(x-1);
g″(x)=
;
令h(x)=2lnx-2x+2;
故h′(x)=
-2;
∵x∈(1,2],
∴
-2<0;
故h(x)在(1,2]上是减函数,
故h(x)<h(1)=0-2+2=0;
故g″(x)<0;
故g′(x)=ln
2x+2lnx-2(x-1)在(1,2]上是减函数;
故g′(x)<0+0-2(1-1)=0;
故g(x)=xln
2x-(x-1)
2在(1,2]上是减函数;
故g(x)<g(1)=0;
故f′(x)<0;
故f(x)=
-
在(1,2]上是减函数;
又∵
(
-
)
=
=
=
=
;
故a≥
;
故a最小值为
.
点评:本题考查了导数的综合应用及恒成立问题,通过不断求导确定函数的单调性,属于中档题.



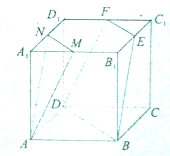 棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.
棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.