练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    乙．


    （1）解：设等差数列{an}的公差为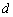，等比数列{bn}的公比为，

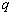    依题意，得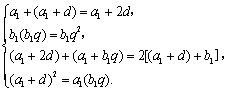   解得a1=d=1，b­1=q=2．

    故an=n，bn=2n．…

    （2）解：将a1，b1，b2记为第1组，a2，a3，a4，b3，b4，b5，b6记为第2组，a5，a6，a7，a8，a9，b7，b8，b9，b10，b11，b12记为第3组，……以此类推，则第n组中，有2n－1项选取于数列{an}，有2 n项选取于数列{bn}，前n组共有n2项选取于数列{an}，有n2＋n项选取于数列{bn}，记它们的总和为Pn，并且有．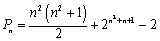

    ，

    ．

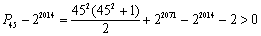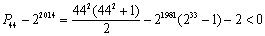    当＋（2＋22＋…＋22012）时，

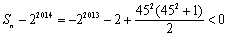    ．当＋（2＋22＋…＋22013)时，

    ．

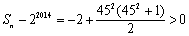    可得到符合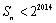的最大的n=452＋2012=4037．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


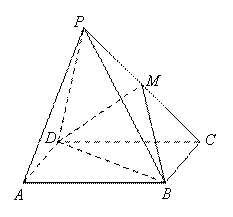
    如图，在四棱锥P - ABCD中，四边形ABCD是矩形，平面PCD⊥平面ABCD，M为PC中点．求证：

    （1）PA∥平面MDB；

    （2）PD⊥BC．

     



    查看答案和解析>>

    科目：高中数学 来源： 题型：


    过椭圆()的左焦点作轴的垂线交椭圆于点，为右焦点，若，则椭圆的离心率为(   ).

       A．          B．          C．           D．  

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    {3，5}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     设实数，满足则的最大值是    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    等比数列{an}的首项为2，公比为3，前n项和为Sn．若log3［an(S4m+1)］=9，则+的最小值是    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a为实常数，y=f(x)是定义在(－∞，0)∪(0，+∞)上的奇函数，且当x<0时，f(x)=2x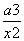－+1．

    （1）求函数f(x)的单调区间；

    （2）若f(x)≥a－1对一切x＞0成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知向量=(1, x )，=(x-1, 2),  若∥, 则x=

        A．-1或2                     B．-2或1     C．1或2             D．-1或-2  

    查看答案和解析>>

    同步练习册答案