
 PMN的面积为
PMN的面积为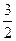 ,点A的坐标为(1+
,点A的坐标为(1+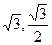 ),
), 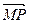 =m·
=m·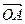 (m为常数),
(m为常数),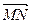
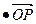
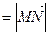
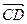 的比分别为λ1、λ2,求λ1+λ2的值。
的比分别为λ1、λ2,求λ1+λ2的值。 =(2c,0)·(x0,y0)=2cx0,
=(2c,0)·(x0,y0)=2cx0, (2c)|y0|=
(2c)|y0|=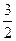 ,y0=
,y0= . ②
. ② =(x0+c,y0),
=(x0+c,y0),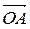 =(1+
=(1+ ),由已知(x0+c,y0)=m(1+
),由已知(x0+c,y0)=m(1+ ),即
),即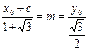 .
.  (x0+c)=(1+
(x0+c)=(1+ )y0. ③
)y0. ③ (1+c)=(1+
(1+c)=(1+ )·
)· ,c2+c-(3+
,c2+c-(3+ )=0,(c-
)=0,(c- )(c+
)(c+ +1)=0,
+1)=0, ,y0=
,y0= .
.  =1(a>b>0).
=1(a>b>0). )在椭圆上,
)在椭圆上,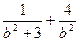 =1.故b2=1,a2=4.
=1.故b2=1,a2=4. +y2="1. " 6分
+y2="1. " 6分
 x+1),
x+1), +y2=1,
+y2=1,
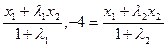 ,
,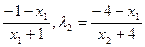 . 9分
. 9分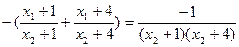 [2x1x2+5(x1+x2)+8],
[2x1x2+5(x1+x2)+8],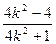 +5·
+5· (8k2-8-40k2+32k2+8)=0,
(8k2-8-40k2+32k2+8)=0, n≥2时,an=Sn-Sn-1=2an-4-2an-1+4,
n≥2时,an=Sn-Sn-1=2an-4-2an-1+4, =1.
=1. }是以1为首项,以1为公差的等差数列.
}是以1为首项,以1为公差的等差数列. =1+(n-1)×1=n∴bn="n·2n. " 6分
=1+(n-1)×1=n∴bn="n·2n. " 6分 n·2n+1,
n·2n+1, ∴Tn="(n-1)·2n+1+2. " 12分
∴Tn="(n-1)·2n+1+2. " 12分

科目:高中数学 来源:不详 题型:解答题
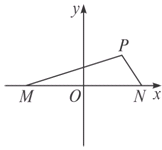
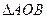 的顶点A在射线
的顶点A在射线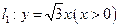 上,
上,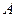 、
、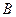 两点关于x轴对称,0为坐标原点,
两点关于x轴对称,0为坐标原点,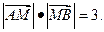 当点A在
当点A在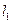 上移动时,记点M的轨迹为W.
上移动时,记点M的轨迹为W.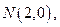 是否存在过
是否存在过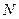 的直线
的直线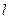 与W相交于P,Q两点,使得
与W相交于P,Q两点,使得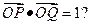 若存在,
若存在,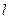 ;若不存在,说明理由.
;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
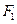 、
、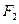 分别是椭圆C:
分别是椭圆C: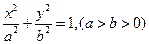 的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过
的左焦点和右焦点,O是坐标系原点, 且椭圆C的焦距为6, 过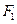 的弦AB两端点A、B与
的弦AB两端点A、B与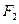 所成
所成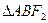 的周长是
的周长是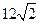 .
.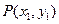 ,
,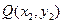 是椭圆C上不同的两点,线段
是椭圆C上不同的两点,线段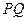 的中点为
的中点为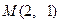 ,
,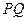 的方程
的方程查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.直线 | B.抛物线 | C.双曲线 | D.圆 |
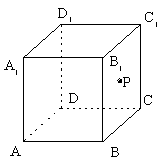
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
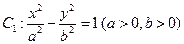 的左、右焦点分别为
的左、右焦点分别为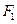 、
、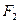 ,抛物线
,抛物线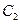 的
的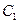 的左准线重合,若双曲线
的左准线重合,若双曲线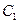 与抛物线
与抛物线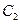 的交点
的交点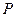 满
满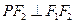 ,则双曲线
,则双曲线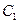 的离心率为
的离心率为| A. | B. | C. | D.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com