
【题目】下列命题中错误的是( )
A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β
B.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β
C.如果直线a∥平面α,那么a平行于平面α内的无数条直线
D.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
【答案】B
【解析】解:A、如图,平面α⊥平面β,α∩β=l,aα,若a∥l,则a∥β,所以正确;
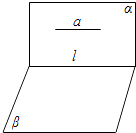
B、如A中的图,平面α⊥平面β,α∩β=l,lα,l不垂直于平面β,所以不正确;
C、根据线面平行的定义,可知C正确;
D、若平面α内存在直线垂直于平面β,根据面面垂直的判定,则有平面α垂直于平面β,与平面α不垂直于平面β矛盾,所以,如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β,正确;
故选:B.
【考点精析】根据题目的已知条件,利用空间中直线与平面之间的位置关系和平面与平面之间的位置关系的相关知识可以得到问题的答案,需要掌握直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点;两个平面平行没有交点;两个平面相交有一条公共直线.


 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
【题目】某市举行“中学生诗词大赛”海选,规定:成绩大于或等于90分的具有参赛资格.某校有800名学生参加了海选,所有学生的成绩均在区间[30,150]内,其频率分布直方图如图:
(Ⅰ)求获得参赛资格的人数;
(Ⅱ)若大赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛.已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为 ![]() ,求甲在初赛中答题个数X的分布列及数学期望E(X)
,求甲在初赛中答题个数X的分布列及数学期望E(X)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求证: ![]() ;
;
(3)判断曲线y=f(x)是否位于x轴下方,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( ) 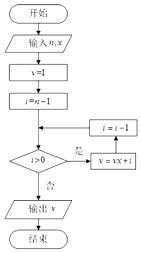
A.5
B.12
C.25
D.50
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥S﹣ABCD的底面ABCD是正方形,各侧棱长与底面的边长均相等,M为SA的中点,则直线BM与SC所成的角的余弦值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥ABCD﹣A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C. 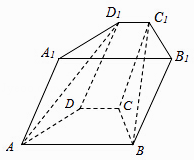
(1)求证:AD1⊥BC;
(2)若直线DD1与直线AB所成角为 ![]() ,求平面ABC1D1与平面ABCD所成角(锐角)的余弦值函数值.
,求平面ABC1D1与平面ABCD所成角(锐角)的余弦值函数值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 若存在互不相同的四个实数0<a<b<c<d满足f(a)=f(b)=f(c)=f(d),则ab+c+2d的取值范围是( )
若存在互不相同的四个实数0<a<b<c<d满足f(a)=f(b)=f(c)=f(d),则ab+c+2d的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,15)
,15)
C.[ ![]() ,15]
,15]
D.( ![]() ,15)
,15)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公比为q的等比数列{an}的前6项和S6=21,且4a1 , ![]() ,a2成等差数列.
,a2成等差数列.
(1)求an;
(2)设{bn}是首项为2,公差为﹣a1的等差数列,记{bn}前n项和为Tn , 求Tn的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com