Question

20．方程$\sqrt{1-{x}^{2}}$=k（x-1）+2有两个不等实根，则k的取值范围是（　　）

• A． （$\frac{3}{4}$，+∞）
• B． （$\frac{1}{3}$，1]
• C． （0，$\frac{3}{4}$）
• D． （$\frac{3}{4}$，1]

Answer 1

分析 由题意可得，函数y=$\sqrt{1-{x}^{2}}$的图象和直线y=k（x-1）+2有2个交点，数形结合求得k的范围．

解答 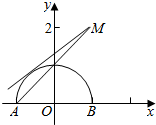解：方程$\sqrt{1-{x}^{2}}$=k（x-1）+2有两个不等实根，
即函数y=$\sqrt{1-{x}^{2}}$的图象和直线y=k（x-1）+2有2个交点．
而函数y=$\sqrt{1-{x}^{2}}$的图象是以原点为圆心，半径等于1的上半圆
（位于x轴及x轴上方的部分），
直线y=k（x-1）+2，即kx-y+2-k=0 的斜率为k，且经过点M（1，2），
当直线和半圆相切时，由$\frac{|0+0+2-k|}{\sqrt{1+{k}^{2}}}$=1，求得k=$\frac{3}{4}$．
当直线经过点A（-1，0）时，由0=k（-1-2）+3求得k=1．
数形结合可得k的范围为（$\frac{3}{4}$，1]，
故选：D．

点评 本题主要考查方程的根的存在性及个数判断，体现了函数和方程的转化及数形结合的数学思想，属于中档题．