
����Ŀ��2017��3��14�գ���ofo�������������������ߺ���ofo���������ֱ����г�����С�Ƴ�����ȫ���һ������������ƽ̨����������������������ģʽ����ز������Ը���Ŀ���п��ˣ����˵�Ӳ��ָ���ǣ�����Ը���Ŀ������ָ��������0.8���������Ŀ��������ģ��ò���Ϊ���˽�����Ը���Ŀ������̶ȣ����������ʹ�ù���������100������������100������Ը���Ŀ����̶ȵ����֣�����������Ƶ�ʷֲ�ֱ��ͼ�� 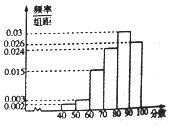
��I��Ϊ���˽ⲿ������ԡ��������������ֽϵ͵�ԭ�ò��Ŵ����ֵ���60�ֵ������������ȡ2�˽�����̸������2������ǡ�ö���[50��60���ĸ��ʣ�
��II����������ѧ��ͳ��֪ʶ���жϸ���Ŀ�ܷ�ͨ�����ˣ���˵�����ɣ�
��ע������ָ��= ![]() ��
��
���𰸡��⣺��I��������ã�������[40��50����[50��60����Ƶ�ʷֱ�Ϊ0.02��0.03��
����������[40��50����[50��60��������ֱ���2����3������ΪA1��A2��B1��B2��B3
�����ֵ���6��0�֣��������������ȡ2�ˣ����п��ܵĽ������10�֣�
������{A1��A2}��{A1��B1}��{A1��B2}��{A1��B3}��{A2��B1}��{A2��B2}��{A2��B3}��{B1��B2}��{B1��B3}��{B2��B3}��
����2�����ֶ���[50��60���������֣���{B1��B2}��{B1��B3}��{B2��B3}��
������ĸ���Ϊ ![]() ��
��
��II����������Ƶ�ʷֲ�ֱ��ͼ�ɵ�����̶ȵ�ƽ���÷�Ϊ45��0.02+55��0.03+65��0.15+75��0.24+85��0.3+95��0.26=80.5��
�ɹ������������ָ��Ϊ ![]() ��
��
���Ը���Ŀ��ͨ�����գ�
����������I�������оٷ�ȷ�������¼������������2������ǡ�ö���[50��60���ĸ��ʣ���II��������������ָ�����ɵý��ۣ�
�����㾫����������Ҫ������Ƶ�ʷֲ�ֱ��ͼ�����֪ʶ�㣬��Ҫ����Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ������ȷ�����⣮


 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() =��cosx����1����
=��cosx����1���� ![]() =��
=�� ![]() sinx��cos2x�����躯��f��x��=
sinx��cos2x�����躯��f��x��= ![]()
![]() +
+ ![]() ��
��
��������f��x������С�����ں͵����������䣻
����x�ʣ�0�� ![]() ��ʱ������f��x����ֵ��
��ʱ������f��x����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ȱ�����{an}�Ĺ���q��1����a1+a3=20��a2=8�� ����������{an}��ͨ�ʽ��
������ ![]() ��Sn������{bn}��ǰn��ͣ�������������n����ʽ
��Sn������{bn}��ǰn��ͣ�������������n����ʽ ![]() ���������ʵ��a��ȡֵ��Χ��
���������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����cos��=�� ![]() �����ǵ������Ľǣ���
�����ǵ������Ľǣ���
��1����sin����+ ![]() ����ֵ��
����ֵ��
��2����tan2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��ABCD�У�����ABCDΪֱ�����Σ�AB��AD��BC��AD����AB=BC=2��AD=3��PA��ƽ��ABCD��PA=2����PB��ƽ��PCD���ɽǵ�����ֵΪ�� �� 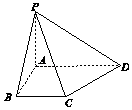
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������p������y=x2+8ax+1��[��1��1]�ϵ���������q������ ![]() =1��ʾ˫���ߣ�������⡰p��q��Ϊ�����⣬��p��q��Ϊ�����⣬��ʵ��a��ȡֵ��Χ��
=1��ʾ˫���ߣ�������⡰p��q��Ϊ�����⣬��p��q��Ϊ�����⣬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������P��ABCD�У�PB�͵���ABCD��CD��PD������ABCDΪֱ�����Σ�AD��BC��AB��BC��AB=AD=PB=3����E����PA�ϣ���PE=2EA�� ����������ֱ��PA��CD���ɵĽǣ�
������֤��PC��ƽ��EBD��
����������A��BE��D�Ĵ�С�����÷����Ǻ�����ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l��x���ϵĽؾ����y���ϵĽؾ��1���ҹ���(6��-2)����ֱ��l�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ABCD�У�PA�͵���ABCD��AB��AD��AC��CD����ABC=60�㣬PA=AB=BC��E��PC���е㣮��֤��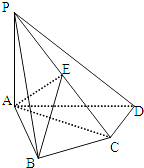
����CD��AE��
����PD��ƽ��ABE��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com