
【题目】四棱锥P﹣ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2,AD=3,PA⊥平面ABCD且PA=2,则PB与平面PCD所成角的正弦值为( ) 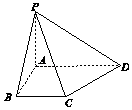
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:依题意,以A为坐标原点,分别以AB,AD,AP 为x,y,z轴建立空间直角坐标系O﹣xyz,AB=BC=2,AD=3,PA=2,则P(0,0,2),
B(2,0,0),C(2,2,0),D(0,3,0),
从而 ![]() =(2,0,﹣2),
=(2,0,﹣2), ![]() =(2,2,﹣2),
=(2,2,﹣2), ![]() =(0,3,﹣2),
=(0,3,﹣2),
设平面PCD的法向量为 ![]() =(a,b,c),
=(a,b,c), ![]() 即
即 ![]() ,
,
不妨取c=3,则b=2,a=1,
所以平面PCD的一个法向量为 ![]() =(1,2,3),
=(1,2,3),
所以PB与平面PCD所成角的正弦值
sinθ=|cos< ![]() ,
, ![]() >|=|
>|=| ![]() |=|-
|=|- ![]() |=
|= ![]() ,
,
故选:B.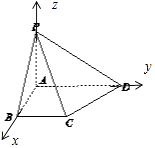
【考点精析】关于本题考查的空间角的异面直线所成的角,需要了解已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 才能得出正确答案.
才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】一个样本M的数据是x1 , x2 , ,xn , 它的平均数是5,另一个样本N的数据x12 , x22 , ,xn2它的平均数是34.那么下面的结果一定正确的是( )
A.SM2=9
B.SN2=9
C.SM2=3
D.Sn2=3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C的对边分别是a,b,c且满足(2a﹣c)cosB=bcosC,
(1)求角B的大小;
(2)若△ABC的面积为为 ![]() 且b=
且b= ![]() ,求a+c的值.
,求a+c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(3x+ ![]() ).
).
(1)求f(x)的单调递增区间;
(2)若α是第二象限角,f( ![]() )=
)= ![]() cos(α+
cos(α+ ![]() )cos2α,求cosα﹣sinα的值.
)cos2α,求cosα﹣sinα的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年3月14日,“ofo共享单车”终于来到芜湖,ofo共享单车又被亲切称作“小黄车”是全球第一个无桩共享单车平台,开创了首个“单车共享”模式.相关部门准备对该项目进行考核,考核的硬性指标是:市民对该项目的满意指数不低于0.8,否则该项目需进行整改,该部门为了了解市民对该项目的满意程度,随机访问了使用共享单车的100名市民,并根据这100名市民对该项目满意程度的评分,绘制了如下频率分布直方图: 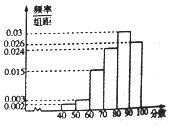
(I)为了了解部分市民对“共享单车”评分较低的原因,该部门从评分低于60分的市民中随机抽取2人进行座谈,求这2人评分恰好都在[50,60)的概率;
(II)根据你所学的统计知识,判断该项目能否通过考核,并说明理由.
(注:满意指数= ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asinxbcosx(a、b为常数,a≠0,x∈R)在x= ![]() 处取得最小值,则函数y=f(
处取得最小值,则函数y=f( ![]() x)是( )
x)是( )
A.偶函数且它的图象关于点(π,0)对称
B.偶函数且它的图象关于点 ![]() 对称
对称
C.奇函数且它的图象关于点 ![]() 对称
对称
D.奇函数且它的图象关于点(π,0)对称
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(-1,1),B(1,1),C(2, ![]() +1),
+1),
(1)求直线AB和AC的斜率.
(2)若点D在线段AB(包括端点)上移动时,求直线CD的斜率的变化范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com