
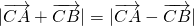
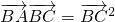
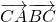 =2SA•cosC,(其中SA表示△ABC的面积)
=2SA•cosC,(其中SA表示△ABC的面积) |=|
|=| |,故四边形ABDC为矩形,故∠ACB为直角,即三角形为直角三角形,本选项不合题意;
|,故四边形ABDC为矩形,故∠ACB为直角,即三角形为直角三角形,本选项不合题意; |,表示出cosB,根据锐角三角形函数定义得出角C为直角,即三角形ABC为直角三角形,本选项不合题意;
|,表示出cosB,根据锐角三角形函数定义得出角C为直角,即三角形ABC为直角三角形,本选项不合题意;
 +
+ |=|
|=| |,|
|,| -
- |=|
|=| |,
|, ,即|
,即| |=|
|=| |,
|, cos
cos =0,
=0,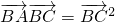 变为为:|
变为为:| |•|
|•| |cosB=|
|cosB=| |2,
|2, |•cosB=|
|•cosB=| |,即cosB=
|,即cosB=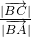 ,
,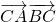 =|
=| |•|
|•| |cos(180°-C)=-|
|cos(180°-C)=-| |•|
|•| |cosC,
|cosC, |
| |•|
|•| |sinC,且
|sinC,且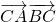 =2SA•cosC,
=2SA•cosC,

科目:高中数学 来源: 题型:
| cosA |
| a |
| cosB |
| b |
| cosC |
| c |
查看答案和解析>>
科目:高中数学 来源:2011年浙江省宁波市海曙区效实中学高考数学模拟试卷(文科)(解析版) 题型:选择题

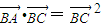
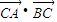 =2SA•cosC,(其中SA表示△ABC的面积)
=2SA•cosC,(其中SA表示△ABC的面积)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com