
分析 (I)将点代入抛物线方程求得p,求得焦点坐标,代入椭圆方程,即可求得a和b的值,求得椭圆C1的方程;
(II)方法一:设直线AC的方程为x=my+1,代入椭圆方程,利用韦达定理及中点坐标公式,求得G,求得OG,代入椭圆方程求得B点坐标,利用点到直线的距离公式,SOABC=$\frac{1}{2}$|AC|(d1+d2),利用函数单调性即可求得四边形OABC的面积S的最小值;
方法二:当直线斜率不存在时,直线AC方程x=1,此时四边形OABC的面积S=$\frac{3}{2}$×2=3,当直线AC的斜率存在时,代入椭圆方程,利用韦达定理及中点坐标公式,求得G,求得OG,代入椭圆方程求得B点坐标,利用点到直线的距离公式,SOABC=$\frac{1}{2}$|AC|(d1+d2),利用函数单调性即可求得四边形OABC的面积S的最小值;
解答 解:(I)∵将($\frac{2}{3}$,$\frac{2}{3}$$\sqrt{6}$)代入抛物线方程,
解得:p=2,
∴y2=4x,
∴椭圆C1的右焦点为(1,0),
∴$\left\{\begin{array}{l}{a^2}-{b^2}=1\\ \frac{{\frac{4}{9}}}{a^2}+\frac{{\frac{24}{9}}}{b^2}=1\end{array}\right.$,
∴$椭圆{C_1}的标准方程为:\frac{x^2}{4}+\frac{y^2}{3}=1$;
(II)方法一:设A(x1,y1),C(x2,y2),G(x0,y0).
设直线AC的方程为x=my+1,
$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,整理得:(4+3m2)y2+6my-9=0,
∴y1+y2=-$\frac{6m}{4+3{m}^{2}}$,y1y2=-$\frac{9}{4+3{m}^{2}}$,
由弦长公式可得|AC|=$\sqrt{1+{m}^{2}}$|y1-y2|=$\sqrt{1+{m}^{2}}$×$\sqrt{({y}_{1}+{y}_{2})^{2}-4{y}_{1}{y}_{2}}$=$\frac{12(1+{m}^{2})}{4+3{m}^{2}}$,
又y0=$\frac{{y}_{1}+{y}_{2}}{2}$=-$\frac{3m}{4+3{m}^{2}}$,x0=my0+1=$\frac{4}{3{m}^{2}+4}$,
∴G($\frac{4}{3{m}^{2}+4}$,-$\frac{3m}{4+3{m}^{2}}$),
直线OG的方程为y=-$\frac{3m}{4}$x,代入椭圆方程得x2=$\frac{16}{4+3{m}^{2}}$,
∴B($\frac{4}{\sqrt{4+3{m}^{2}}}$,-$\frac{3m}{\sqrt{4+3{m}^{2}}}$),
B到直线AC的距离d1=$\frac{\sqrt{4+3{m}^{2}}-1}{1+{m}^{2}}$,
O到直线AC的距离d2=$\frac{1}{\sqrt{1+{m}^{2}}}$,
∴SOABC=$\frac{1}{2}$|AC|(d1+d2)=$\frac{1}{2}$×$\frac{12(1+{m}^{2})}{4+3{m}^{2}}$×$\frac{\sqrt{4+3{m}^{2}}}{\sqrt{1+{m}^{2}}}$=6×$\sqrt{\frac{1+{m}^{2}}{4+3{m}^{2}}}$=6$\sqrt{\frac{1}{3}-\frac{1}{3(4+3{m}^{2})}}$≥3,
当m=0时取得最小值3.
∴四边形OABC的面积S的最小值3.
方法二:当直线斜率不存在时,直线AC方程x=1,此时四边形OABC的面积S=$\frac{3}{2}$×2=3,
当直线AC的斜率存在时,设A(x1,y1),C(x2,y2),
直线AC:y=k(x-1),$\left\{\begin{array}{l}{y=k(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,整理得:(3+4k2)x2-8k2x+4k2-12=0,
则x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
xG=$\frac{{x}_{1}+{x}_{2}}{2}$=$\frac{4{k}^{2}}{3+4{k}^{2}}$,yG=k(xG-1)=$\frac{-3k}{3+4{k}^{2}}$,
则G($\frac{4{k}^{2}}{3+4{k}^{2}}$,$\frac{-3k}{3+4{k}^{2}}$),则OG:y=-$\frac{3}{4k}$x,
则$\left\{\begin{array}{l}{y=-\frac{3}{4k}x}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,解得:x2=$\frac{16{k}^{2}}{4{k}^{2}+3}$,
不妨设k>0,
则$\left\{\begin{array}{l}{{x}_{B}=\frac{4k}{\sqrt{3+4{k}^{2}}}}\\{{y}_{B}=\frac{-3}{\sqrt{3+4{k}^{2}}}}\end{array}\right.$,
则B到直线AC距离d1=$\frac{丨\sqrt{3+4{k}^{2}-k}丨}{\sqrt{1+{k}^{2}}}$=$\frac{\sqrt{3+4{k}^{2}}-k}{\sqrt{1+{k}^{2}}}$,
O到直线AC的距离d2=$\frac{k}{\sqrt{1+{k}^{2}}}$,
由弦长公式可知丨AC丨=$\sqrt{1+{k}^{2}}$$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$$\sqrt{\frac{16(9{k}^{2}+9)}{(3+4{k}^{2})^{2}}}$,
=$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$,
则SOABC=$\frac{1}{2}$|AC|(d1+d2)=$\frac{1}{2}$×$\frac{12(1+{k}^{2})}{3+4{k}^{2}}$×$\frac{\sqrt{3+4{k}^{2}}}{\sqrt{1+{k}^{2}}}$,
=6×$\sqrt{\frac{1+{k}^{2}}{3+4{k}^{2}}}$,
=6×$\sqrt{\frac{1}{4}+\frac{1}{4{(4k}^{2}+3)}}$>3,
综上可知:当直线AC垂直于x轴时,四边形OABC的面积S的最小值3.
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,韦达定理,中点坐标公式,点到直线的距离公式,弦长公式,考查函数的单调性与椭圆的综合应用,考查计算能力,属于中档题.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | (-1,0)∪(0,1) | B. | (-∞,1)∪(1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-∞,-1)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 26 | B. | 32 | C. | 36 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
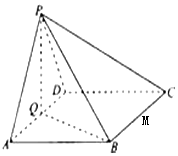 如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.
如图,四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q是AD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com