
| A. | $[-1,-\frac{1}{3}]$ | B. | $[-\frac{1}{3},\frac{1}{3}]$ | C. | [-1,1] | D. | $[-1,\frac{1}{3}]$ |
分析 求出函数f(x)的导数f′(x)=x-$\frac{1}{3}$sin2xt+tsinx在R上单调递增可转化为f″(x)=-$\frac{4}{3}$cos2x+tcosx+$\frac{5}{3}$≥0,在R上恒成立,利用分离参数法即可求解.
解答 解:f′(x)=x-$\frac{1}{3}$sin2xt+tsinx在R上单调递增,
即f″(x)=-$\frac{4}{3}$cos2x+tcosx+$\frac{5}{3}$≥0,在R上恒成立,
令m=cosx,m∈[-1,1],-$\frac{4}{3}$m2+tm+$\frac{5}{3}$≥0⇒tm≥$\frac{4}{3}$m2-$\frac{5}{3}$,
当m=0时,成立;当m∈(0,1]时,t≥$\frac{4}{3}$m-$\frac{5}{3m}$,
函数g(m)=$\frac{4}{3}$m-$\frac{5}{3m}$在(0,1]上是增函数,
∴t≥g(1)=-$\frac{1}{3}$;当m∈[-1,0)时,t≤$\frac{4}{3}$m-$\frac{5}{3m}$,
∵函数g(m)=$\frac{4}{3}$m-$\frac{5}{3m}$在[-1,0(上是增函数,t≤g(-1)=$\frac{1}{3}$,
综上则实数t的取值范围为[-$\frac{1}{3},\frac{1}{3}$].
故选B.
点评 本题考查了三角函数的变形以及由函数单调性的性质求参数的范围.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的 浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的 浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
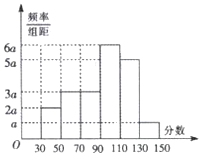 从某市高三数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:
从某市高三数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 容量,方差 | B. | 容量,平均数 | C. | 平均数,容量 | D. | 标准差,平均数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=-x2-2x+12 | B. | f(x)=x2-2x+10 | C. | f(x)=-x2+2x+8 | D. | f(x)=x2+2x+6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 无穷多个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com