
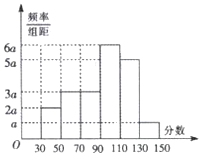
 从某市高三数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:
从某市高三数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:分析 (Ⅰ)根据平均数是频率分布直方图各个小矩形的面积×底边中点横坐标之和,求出本次考试的平均分;
(Ⅱ)利用频数=频率×样本数,求出分数在[30,50)和[130,150]的学生人数,再按照分层抽样的方法按比例求出3人中成绩在[130,150]的有几人?
(III)由(II)知,抽取的3人中分数在[30,50)的有2人,分数在[130,150]的有1人,问题为古典概型.
解答 解:(Ⅰ)由题意(a+2a+3a+3a+5a+6a)×20=1,∴a=0.0025
由频率分布直方图,得该校高三学生本次数学考试的平均分为
0.0050×20×40+0.0075×20×60+0.0075×20×80+0.0150×20×100
+0.0125×20×120+0.0025×20×140=92.
(Ⅱ)样本中分数在[30,50)和[130,150]的学生人数分别为6人和3人,
所以抽取的3人中成绩在[130,150]的有3×$\frac{3}{9}$=1人.
(III)由(II)知,抽取的3人中分数在[30,50)的有2人,记为a,b,
分数在[130,150]的有1人,记为c,从中随机抽取2人,总的情形有(a,b),(a,c),(b,c)三种.
而分数在[30,50)和[130,150]各1人的情形为(a,c),(b,c)两种,
故所求的概率为:P=$\frac{2}{3}$.
点评 本题考查频率分布直方图的基础知识,分层抽样,古典概型求解.融合了基本知识,难度不大,但是好题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 6 | C. | $\sqrt{3}$ | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “∥”后面是注释内容,对程序运行起着重要作用 | |
| B. | “∥”后面是程序执行的指令,对程序运行起着重要作用 | |
| C. | “∥”后面是注释内容,对程序运行不起作用 | |
| D. | “∥”后面是程序执行的指令,对程序运行不起作用 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-1,-\frac{1}{3}]$ | B. | $[-\frac{1}{3},\frac{1}{3}]$ | C. | [-1,1] | D. | $[-1,\frac{1}{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com