
分析 把直线的方程与椭圆的方程联立,转化为关于x的一元二次方程,得到根与系数的关系,假设以CD为直径的圆过E点,则CE⊥DE,将它们联立消去x1,x2即可得出k的值.
解答 解:假若存在这样的k值,由$\left\{\begin{array}{l}y=kx+2\\{x^2}+3{y^2}-3=0\end{array}\right.$得(1+3k2)x2+12kx+9=0.
∴△=(12k)2-36(1+3k2)>0. ①
设C(x1,y1)、D(x2,y2),则$\left\{\begin{array}{l}{x_1}+{x_2}=-\frac{12k}{{1+3{k^2}}}\\{x_1}•{x_2}=\frac{9}{{1+3{k^2}}}\end{array}\right.$②
而${y_1}•{y_2}=(k{x_1}+2)(k{x_2}+2)={k^2}{x_1}{x_2}+2k({x_1}+{x_2})+4$.
要使以CD为直径的圆过点E(-1,0),当且仅当CE⊥DE时,则$\frac{y_1}{{{x_1}+1}}•\frac{y_2}{{{x_2}+1}}=-1$,即y1y2+(x1+1)(x2+1)=0.
∴(k2+1)x1x2+2(k+1)(x1+x2)+5=0. ③
将②式代入③整理解得$k=\frac{7}{6}$.经验证,$k=\frac{7}{6}$,使①成立.
综上可知,存在$k=\frac{7}{6}$,使得以CD为直径的圆过点E.
点评 本题考查椭圆的标准方程,考查椭圆的性质,考查直线与椭圆的位置关系,考查韦达定理的运用,考查向量知识,解题的关键是联立方程,利用韦达定理求解.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{4}$) | B. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{4}$] | C. | [0,-$\frac{\sqrt{3}}{4}$] | D. | (-$\frac{2}{3}$,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a2-a+1)<$f(\frac{3}{4})$ | B. | f(a2-a+1)>$f(\frac{3}{4})$ | C. | f(a2-a+1)≤$f(\frac{3}{4})$ | D. | f(a2-a+1)≥$f(\frac{3}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 顾客人数/商品 | 甲 | 乙 | 丙 | 丁 |
| 100 | √ | × | √ | √ |
| 217 | × | √ | × | √ |
| 200 | √ | √ | √ | × |
| 300 | √ | × | √ | × |
| 85 | √ | × | × | × |
| 98 | × | √ | × | × |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
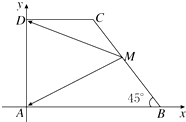 在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=45°,AB=2CD=4,M为腰BC的中点,则$\overrightarrow{MA}$•$\overrightarrow{MD}$=( )
在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=45°,AB=2CD=4,M为腰BC的中点,则$\overrightarrow{MA}$•$\overrightarrow{MD}$=( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-∞,1] | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
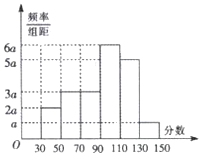 从某市高三数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:
从某市高三数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com