
分析 当a≤0时,f(a)=$\frac{1}{2}a+1$=-1;当a>0时,f(a)=-(a-1)2=-1.由此能求出使f(a)=-1成立的a值.
解答 解:∵f(x)=$\left\{\begin{array}{l}\frac{1}{2}x+1,x≤0\\-{(x-1)^2},x>0\end{array}$,f(a)=-1,
∴当a≤0时,f(a)=$\frac{1}{2}a+1$=-1,解得a=-4.
当a>0时,f(a)=-(a-1)2=-1,解得a=2或a=0(舍).
∴使f(a)=-1成立的a值是-4或2.
故答案为:-4或2.
点评 本题考查函数值的求法及应用,是基础题,解题时要认真审题,注意函数性质的合理运用.


科目:高中数学 来源: 题型:选择题
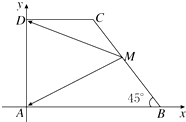 在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=45°,AB=2CD=4,M为腰BC的中点,则$\overrightarrow{MA}$•$\overrightarrow{MD}$=( )
在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=45°,AB=2CD=4,M为腰BC的中点,则$\overrightarrow{MA}$•$\overrightarrow{MD}$=( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{n}^{3}}{3}+\frac{{n}^{2}}{2}+\frac{n}{6}+1+\frac{1}{{2}^{n}}$ | B. | $\frac{{n}^{3}}{3}+\frac{{n}^{2}}{2}+\frac{n}{6}+1$-$\frac{1}{{2}^{n}}$ | ||
| C. | $\frac{{n}^{3}}{3}+\frac{{n}^{2}}{2}+\frac{n}{6}+1$+$\frac{1}{{2}^{n-1}}$ | D. | $\frac{{n}^{3}}{3}+\frac{{n}^{2}}{2}+\frac{n}{6}+1$-$\frac{1}{{2}^{n-1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{y^2}{5}+\frac{x^2}{4}=1$ | B. | $\frac{x^2}{12}+\frac{y^2}{3}=1$ | C. | x2=-12y | D. | $\frac{y^2}{6}-\frac{x^2}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
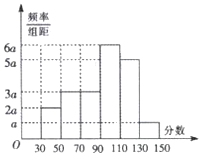 从某市高三数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:
从某市高三数学考试成绩中,随机抽取了60名学生的成绩得到频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$ | B. | 2$\sqrt{5}$ | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 容量,方差 | B. | 容量,平均数 | C. | 平均数,容量 | D. | 标准差,平均数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$或$\frac{5π}{6}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com