
 是奇函数,则下列命题是真命题的是( )
是奇函数,则下列命题是真命题的是( ) 的定义域是(-1,1),且f(-x)=ln
的定义域是(-1,1),且f(-x)=ln =-ln
=-ln =-f(x),所以该函数是奇函数.
=-f(x),所以该函数是奇函数. (a>0,且a≠1,b≠0)的函数是奇函数;复合命题p且q的真假关系可记为:一假即假,复合命题p或q的真假关系可记为:一真即真.
(a>0,且a≠1,b≠0)的函数是奇函数;复合命题p且q的真假关系可记为:一假即假,复合命题p或q的真假关系可记为:一真即真. 

 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源:2014届四川省外语实验学校高高二4月月考文科数学试卷解析版 题型:选择题
设 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
①若 ,
, ,则
,则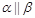 ;
;
②若 ,
, ,
, ,
, ,则
,则 ;
;
③若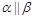 ,
, ,则
,则 ;
;
④若 ,
, ,
, ,
, ,则
,则 其中真命
其中真命
题的个数是 ( )))
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高一第二学期期中考试数学试卷(解析版) 题型:选择题
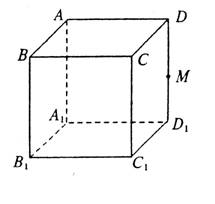
如图,M是正方体ABCD—A1B1C1D1的棱DD1的中点,给出下列四个命
题:
①过M点有且只有一条直线与直线AB、B1C1都相交
②过M点有且只有一条直线与直线AB、B1C1都垂直
③过M点有且只有一个平面与直线AB、B1C1都相交
④过M点有且只有一个平面与直线AB、B1C1都平行
其中真命题的个数是( )
A、1 B、2 C、3 D、4
查看答案和解析>>
科目:高中数学 来源: 题型:
设m,n是两条不同的直线,α、β、γ是三个不同的平面给出下列四个命
题:
①若m⊥α,n∥α,则m⊥n; ②若α⊥γ,β⊥γ,则α∥β;
③若m∥α,n∥α,则m∥n; ④若α∥β,β∥γ,m⊥α,则m⊥γ
其中正确命题的序号是:
A.①和② B.②和③ C.③和④ D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
设m,n是两条不同的直线,α、β、γ是三个不同的平面给出下列四个命
题:
①若m⊥α,n∥α,则m⊥n; ②若α⊥γ,β⊥γ,则α∥β;
③若m∥α,n∥α,则m∥n; ④若α∥β,β∥γ,m⊥α,则m⊥γ
其中正确命题的序号是:
A.①和② B.②和③ C.③和④ D.①和④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com