
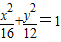 上对两焦点张角为90°的点有( )
上对两焦点张角为90°的点有( )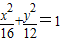 内部,根据圆的几何性质可得椭圆上不存在对两焦点张角为90°的点,从而得到答案.
内部,根据圆的几何性质可得椭圆上不存在对两焦点张角为90°的点,从而得到答案.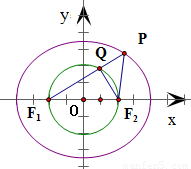
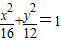 ,∴F1(-2,0),F2(2,0)
,∴F1(-2,0),F2(2,0)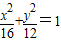 内部
内部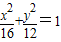 上不存在对两焦点张角为90°的点
上不存在对两焦点张角为90°的点

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源:高二数学 教学与测试 题型:044
P为中心在原点、焦点在x轴上的椭圆上一点,它到此椭圆两焦点的距离之和为4,到两准线的距离之和为8,求此椭圆的方程及焦点对短轴的张角(即焦点与短轴的两个端点连线所成的角).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com