
科目:高中数学 来源:不详 题型:解答题
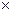 月
月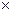 日)将蔬菜送到,则亚运村销售商一次性支付给菜园20万元; 若在约定日期前送到,每提前一天销售商将多支付给菜园1万元; 若在约定日期后送到,每迟到一天销售商将少支付给菜园1万元.
日)将蔬菜送到,则亚运村销售商一次性支付给菜园20万元; 若在约定日期前送到,每提前一天销售商将多支付给菜园1万元; 若在约定日期后送到,每迟到一天销售商将少支付给菜园1万元.| 统计信息 汽车行 驶路线 | 不堵车的情况下到达亚运村乙所需 时间 (天) | 堵车的情况下到达亚运村乙所需时间 (天) | 堵车的 概率 | 运费 (万元) |
| 公路1 | 2 | 3 | 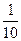 | 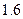 |
| 公路2 | 1 | 4 | 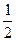 | 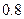 |
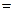 销售商支付给菜园的费用
销售商支付给菜园的费用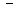 运费)
运费)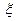 (单位:万元),求
(单位:万元),求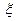 的分布列和数学期望
的分布列和数学期望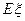 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
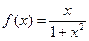 .
. 的奇偶性;
的奇偶性;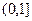 上的单调性,并用单调性定义证明;
上的单调性,并用单调性定义证明;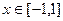 ,
, 恒成立,求实数
恒成立,求实数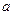 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
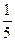 ,以后由于政府重视,积极防治,疫情趋缓,从第二个月起,每一个月的损失是上月损失的
,以后由于政府重视,积极防治,疫情趋缓,从第二个月起,每一个月的损失是上月损失的 .问:
.问: ,问接受了政府补贴后,该养殖户第3个月损失多少元?又问:与(1)相比较,该养殖户在三个月当中总共可减少损失多少元?
,问接受了政府补贴后,该养殖户第3个月损失多少元?又问:与(1)相比较,该养殖户在三个月当中总共可减少损失多少元?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
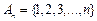 ,映射
,映射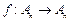 满足:
满足: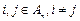 时,
时,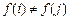 ;
;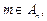 若
若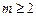 ,则有
,则有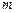
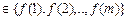 .则称映射
.则称映射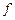 :
: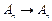 是一个“优映
是一个“优映
|
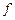 :
: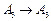 是一个“优映射”.若映射
是一个“优映射”.若映射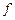 :
: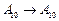 是“优映射”,且方程
是“优映射”,且方程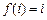 的解恰有6个,则这样的“优映射”的个数是 ( )
的解恰有6个,则这样的“优映射”的个数是 ( )| A.21 | B.42 | C.63 | D.84 |

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 136.135 | 15.552 | -3.92 | 10.88 | -52.488 | -232.064 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com