
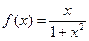 .
. 的奇偶性;
的奇偶性;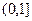 上的单调性,并用单调性定义证明;
上的单调性,并用单调性定义证明;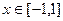 ,
, 恒成立,求实数
恒成立,求实数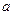 的取值范围.
的取值范围.科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
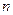 年利润为
年利润为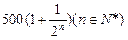 万元。
万元。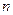 年的利润共
年的利润共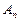 万元;若进行技术改造后,则从2006年起的前
万元;若进行技术改造后,则从2006年起的前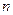 年的纯利润(扣除技术改造600万元资金)共
年的纯利润(扣除技术改造600万元资金)共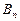 万元,分别求
万元,分别求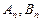 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.10% | B.15% | C.18% | D.20% |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 相等的左中右三个矩形栏目,这三栏的面积之和为60 000
相等的左中右三个矩形栏目,这三栏的面积之和为60 000  ,四周空白的宽度为10 cm,栏与栏之间的中缝空白的宽度为5 cm,怎样确定广告矩形栏目高与宽的尺寸(单位:cm),能使整个矩形广告面积最小.
,四周空白的宽度为10 cm,栏与栏之间的中缝空白的宽度为5 cm,怎样确定广告矩形栏目高与宽的尺寸(单位:cm),能使整个矩形广告面积最小.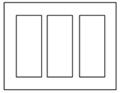
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com