
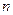 年利润为
年利润为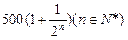 万元。
万元。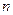 年的利润共
年的利润共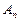 万元;若进行技术改造后,则从2006年起的前
万元;若进行技术改造后,则从2006年起的前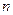 年的纯利润(扣除技术改造600万元资金)共
年的纯利润(扣除技术改造600万元资金)共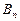 万元,分别求
万元,分别求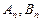 ;
; 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
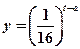 (
(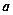 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题: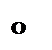

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
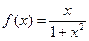 .
. 的奇偶性;
的奇偶性;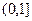 上的单调性,并用单调性定义证明;
上的单调性,并用单调性定义证明;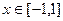 ,
, 恒成立,求实数
恒成立,求实数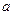 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度
的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度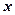 不得
不得 超过
超过 米,房屋正面的造价为400元
米,房屋正面的造价为400元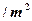 ,房屋侧面的造价为150元
,房屋侧面的造价为150元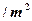 ,屋顶和底面的造价费用合计为5800元,如果墙高为3米.且不计房屋背面的费用.
,屋顶和底面的造价费用合计为5800元,如果墙高为3米.且不计房屋背面的费用. 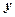 表示成
表示成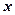 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com