
 的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度
的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度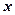 不得
不得 超过
超过 米,房屋正面的造价为400元
米,房屋正面的造价为400元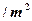 ,房屋侧面的造价为150元
,房屋侧面的造价为150元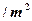 ,屋顶和底面的造价费用合计为5800元,如果墙高为3米.且不计房屋背面的费用.
,屋顶和底面的造价费用合计为5800元,如果墙高为3米.且不计房屋背面的费用. 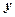 表示成
表示成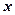 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域; 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
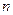 年利润为
年利润为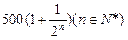 万元。
万元。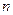 年的利润共
年的利润共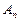 万元;若进行技术改造后,则从2006年起的前
万元;若进行技术改造后,则从2006年起的前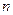 年的纯利润(扣除技术改造600万元资金)共
年的纯利润(扣除技术改造600万元资金)共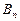 万元,分别求
万元,分别求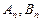 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
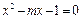 有两个实根
有两个实根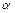 、
、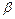 ,且
,且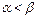 .定义函数
.定义函数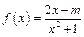 .
.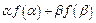 的值;
的值; 在区间
在区间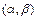 上的单调性,并加以证明;
上的单调性,并加以证明;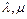 为正实数,证明不等式:
为正实数,证明不等式: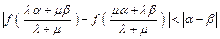 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
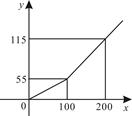
 (元)之间的函数关系如图所示,当月电量为300度时,应交电费( )
(元)之间的函数关系如图所示,当月电量为300度时,应交电费( )| A.165元 | B.170元 | C.175元 | D.180元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 相等的左中右三个矩形栏目,这三栏的面积之和为60 000
相等的左中右三个矩形栏目,这三栏的面积之和为60 000  ,四周空白的宽度为10 cm,栏与栏之间的中缝空白的宽度为5 cm,怎样确定广告矩形栏目高与宽的尺寸(单位:cm),能使整个矩形广告面积最小.
,四周空白的宽度为10 cm,栏与栏之间的中缝空白的宽度为5 cm,怎样确定广告矩形栏目高与宽的尺寸(单位:cm),能使整个矩形广告面积最小.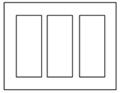
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com