Question

三角形中位线是三角形中的重要线段，它的性质可以为许多问题的证明和求解提供依据，在几何中有着举足轻重的地位，那么如何证明三角形中位线定理呢？

Answer 1

思路:连结三角形两边中点的线段叫做三角形的中位线，这里要明确三角形的中位线和三角形的中线不同(如图1-1-9).三角形中位线定理的内容是:三角形中位线平行于第三边，并且等于它的一半.

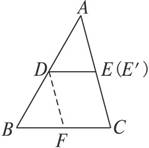
图1-1-9

探究:证明:如图1-1-9，DE是中位线，E是AC的中点，

过点D作DE′∥BC，则E′也是AC的中点，所以E与E′重合，DE′与DE重合.

所以DE∥BC.

同理，过点D作DF∥AC，交BC于F，则BF=FC.

因为DE∥FC，DF∥EC，所以四边形DFCE是平行四边形.

所以DE=FC.

又因为FC=BC，所以DE=BC.

上述过程中，DE′与DE重合是定理证明的关键一步，本推理过程中应用了同一法思想.

该定理的证明，关键在于添加辅助线，如图1-1-10所示的几种辅助线代表几种不同的证法.

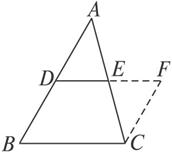
（1）(1)延长中位线DE到F,使EF=DE.

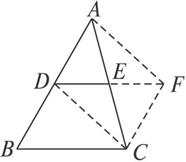
（2）(2)延长中位线DE到F,使EF=DE得ADCF.

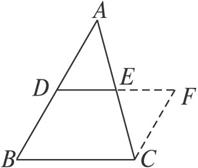
(3)作CF∥AB与DE的延长线交于点F.

图1-1-10

    三角形中位线定理是三角形的一个重要的性质定理，其特点是:同一题设，两个结论.一个结论是表明位置关系的，另一个结论是表明数量关系的，在应用时不一定同时需要两个关系，有时需要平行关系，有时要求倍分关系，可由具体情况按需选用.事实上，平行线等分线段定理的推论1:经过三角形一边中点与另一边平行的直线平分第三边，即三角形中位线判定定理.