
将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,将得到的点数分别记为 .
.
(1)求直线 与圆
与圆 相切的概率;
相切的概率;
(2)将 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
(1)直线 与圆
与圆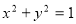 相切的概率为
相切的概率为 ;
;
(2)这三条线段能围成等腰三角形的概率为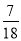 .
.
【解析】
试题分析:(1)先后2次抛掷一枚骰子,将得到的点数分别记为 事件总数为36,直线
事件总数为36,直线 与圆
与圆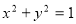 相切只有两种情况,所以相切的概率为
相切只有两种情况,所以相切的概率为 ;
;
(2)总事件共36种,这三条线段能围成等腰三角形有14种情况,故能围成等腰三角形的概率为 .
.
.
试题解析: (1)先后2次抛掷一枚骰子,将得到的点数分别记为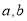 ,事件总数为6×6=36.
,事件总数为6×6=36.
因为直线 与圆
与圆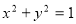 相切,所以有
相切,所以有
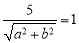 即:
即: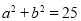 ,由于
,由于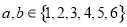
所以,满足条件的情况只有 或
或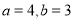 两种情况.
两种情况.
所以,直线 与圆
与圆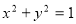 相切的概率是
相切的概率是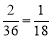
(2)先后2次抛掷一枚骰子,将得到的点数分别记为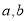 ,事件总数为6×6=36.
,事件总数为6×6=36.
因为,三角形的一边长为5
所以,当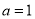 时,
时, ,(1,5,5) 1种
,(1,5,5) 1种
当 时,
时,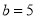 ,(2,5,5) 1种
,(2,5,5) 1种
当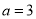 时,
时,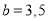 ,(3,3,5),(3,5,5) 2种
,(3,3,5),(3,5,5) 2种
当 时,
时,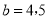 ,(4,4,5),(4,5,5) 2种
,(4,4,5),(4,5,5) 2种
当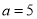 时,
时,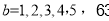 ,
,
(5,1,5),(5,2,5),(5,3,5),
(5,4,5),(5,5,5),(5,6,5) 6种
当 时,
时, ,(6,5,5),(6,6,5) 2种
,(6,5,5),(6,6,5) 2种
故满足条件的不同情况共有14种.
所以,三条线段能围成不同的等腰三角形的概率为 .
.
考点:古典概型、直线与圆的位置关系.


科目:高中数学 来源:2016届山东省济宁市高一3月质量检测数学试卷(解析版) 题型:选择题
设等差数列{an}的前n项和为Sn,若S9>0,S10<0,则 中最大的是( )
中最大的是( )
A.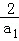 B.
B.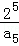 C.
C.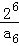 D.
D.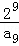
查看答案和解析>>
科目:高中数学 来源:2016届山东省济宁市高一5月质量检测数学试卷(解析版) 题型:选择题
已知函数 的最小正周期为
的最小正周期为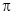 ,则该函数的图象( )
,则该函数的图象( )
A.关于点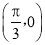 对称 B.关于直线
对称 B.关于直线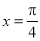 对称
对称
C.关于点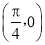 对称 D.关于直线
对称 D.关于直线 对称
对称
查看答案和解析>>
科目:高中数学 来源:2016届山东省济宁市高一3月质量检测数学试卷(解析版) 题型:填空题
给出下列命题:
?存在实数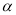 ,使
,使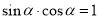
②函数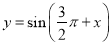 是偶函数
是偶函数
③ 直线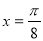 是函数
是函数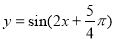 的一条对称轴
的一条对称轴
④若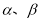 是第一象限的角,且
是第一象限的角,且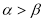 ,则
,则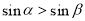
其中正确命题的序号是______________
查看答案和解析>>
科目:高中数学 来源:2016届山东省高一下学期期末模拟检测一数学试卷(解析版) 题型:填空题
已知下列命题:①函数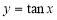 在第一象限是增函数;
在第一象限是增函数;
②函数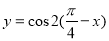 是偶函数; ③函数
是偶函数; ③函数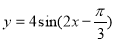 的一个对称中心是(
的一个对称中心是(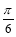 ,0);
,0);
④函数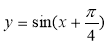 在闭区间
在闭区间 上是增函数;
上是增函数;
写出所有正确的命题的题号: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com