已知函数f(x)=(x2+ax+1)ex,g(x)=(b+2)x2.
(Ⅰ)当a=1时,曲线y=f(x)在点(0,f(0))处的切线恰与曲线y=g(x)相切,求实数b的值;
(Ⅱ)当a=b<0,对任意的x1,x2∈[-1,1],都有f(x1)≥g(x2),求实数b的取值范围.
【答案】
分析:(Ⅰ)求导函数,求出曲线y=f(x)在点(0,f(0))处的切线方程,与y=g(x)联立,利用判别式,可求实数b的值;
(Ⅱ)对任意的x
1,x
2∈[-1,1],都有f(x
1)≥g(x
2),等价于f(x)
min≥g(x)
max,即可求实数b的取值范围.
解答:解:(Ⅰ)f'(x)=[x
2+(a+2)x+a+1]e
x=(x
2+3x+2)e
x,…(2分)
∴f'(0)=2,
∵f(0)=1,∴切线为:y=2x+1,…(4分)
由
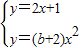
得:(b+2)x
2-2x-1=0,
∴△=4+4(b+2)=0得:b=-3…(6分)
(Ⅱ)f'(x)=(x+1)(x+b+1)e
x=0得:x=-1或x=-1-b,…(7分)
∵b<0,∴-1-b>-1
①当-1-b≥1,即b≤-2时,在[-1,1]上,f'(x)≤0,此时f(x)在[-1,1]单调递减,
∴f(x)
min=f(1)=(b+2)e,此时g(x)
max=g(0)=0,
∴(b+2)e≥0,得:b≥-2.
∴b=-2…(10分)
②当-1-b<1,即-2<b<0时,f(x)在(-1,-1-b)单调递减,(-1-b,1)单调递增,
∴
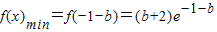
,g(x)
max=g(±1)=b+2,
∴(b+2)e
-1-b≥b+2,得:e
-1-b≥1,∴-2<b≤-1…(13分)
综上可知:-2≤b≤-1…(14分)
点评:本题考查导数知识的运用,考查导数的几何意义,考查恒成立问题,利用f(x)
min≥g(x)
max,是解题的关键.

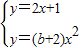 得:(b+2)x2-2x-1=0,
得:(b+2)x2-2x-1=0,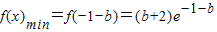 ,g(x)max=g(±1)=b+2,
,g(x)max=g(±1)=b+2,
