
“解方程( ”有如下思路;设
”有如下思路;设 ,则
,则 在R上单调递减,且
在R上单调递减,且 ,故原方程有唯一解x=2,类比上述解题思路,不等式
,故原方程有唯一解x=2,类比上述解题思路,不等式 的解集是 .
的解集是 .
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:填空题
科拉茨是德国数学家,他在1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半(即 );如果n是奇数,则将它乘3加1(即
);如果n是奇数,则将它乘3加1(即 ),不断重复这样的运算,经过有限步后,一定可以得到1.如初始正整数为6,按照上述变换规则,我们可以得到一个数列:6,3,10,5,16,8,4,2,1.对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:
),不断重复这样的运算,经过有限步后,一定可以得到1.如初始正整数为6,按照上述变换规则,我们可以得到一个数列:6,3,10,5,16,8,4,2,1.对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:
(1)如果 ,则按照上述规则施行变换后的第8项为 .
,则按照上述规则施行变换后的第8项为 .
(2)如果对正整数 (首项)按照上述规则施行变换后的第8项为1(注:1可以多次出现),则
(首项)按照上述规则施行变换后的第8项为1(注:1可以多次出现),则 的所有不同值的个数为 .
的所有不同值的个数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
观察下列算式:
13 =1,
23 =3+5,
33 = 7+9+11
43 ="13" +15 +17 +19 ,
… …
若某数n3按上述规律展开后,发现等式右边含有“2013”这个数,则n= .
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
类比平面内正三角形的“三边相等,三内角相等”的性质,可推知正四面体的一些性质:?“各棱长相等,同一顶点上的两条棱的夹角相等;?各个面都是全等的正三角形,相邻两个面所成的二面角相等;?各个面都是全等的正三角形,同一顶点上的任何两条棱的夹角相等。你认为比较恰当的是
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知Sk=1k+2k+3k+…+nk,当k=1,2,3,…时,观察下列等式:
S1= n2+
n2+ n,
n,
S2=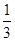 n3+
n3+ n2+
n2+ n,
n,
S3= n4+
n4+ n3+
n3+ n2,
n2,
S4= n5+
n5+ n4+
n4+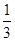 n3-
n3- n,
n,
S5=An6+ n5+
n5+ n4+Bn2,…
n4+Bn2,…
可以推测,A-B=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com