
类比平面内正三角形的“三边相等,三内角相等”的性质,可推知正四面体的一些性质:?“各棱长相等,同一顶点上的两条棱的夹角相等;?各个面都是全等的正三角形,相邻两个面所成的二面角相等;?各个面都是全等的正三角形,同一顶点上的任何两条棱的夹角相等。你认为比较恰当的是
①②③
解析试题分析:本题考查的知识点是类比推理,在由平面几何的性质类比推理空间立体几何性质时,我们常用的思路是:由平面几何中点的性质,类比推理空间几何中线的性质;由平面几何中线的性质,类比推理空间几何中面的性质;由平面几何中面的性质,类比推理空间几何中体的性质;或是将一个二维平面关系,类比推理为一个三维的立体关系,故类比平面内正三角形的“三边相等,三内角相等”的性质,我们可以推断正四面体的相关性质解:在由平面几何的性质类比推理空间立体几何性质时,我们常用的思路是:由平面几何中点的性质,类比推理空间几何中线的性质;由平面几何中线的性质,类比推理空间几何中面的性质;由平面几何中面的性质,类比推理空间几何中体的性质;或是将一个二维平面关系,类比推理为一个三维的立体关系,故类比平面内正三角形的“三边相等,三内角相等”的性质,推断:①各棱长相等,同一顶点上的任两条棱的夹角都相等;②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;③各个面都是全等的正三角形,同一顶点上的任两条棱的夹角都相等.都是恰当的故答案为:①②③
考点:类比推理
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:填空题
从1=1,1-4="-(1+2),1-4+9=1+2+3,1-4+9-16=-(1+2+3+4)," ,推广到第 个等式为_______________.
个等式为_______________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
对大于或等于2的自然数m的3次方幂有如下分解方式: ,
, ,
, ,……
,……
则(1)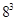 的分解中最小的数是 (2分);
的分解中最小的数是 (2分);
(2)按以上规律,第 个式子可以表示为 (3分).
个式子可以表示为 (3分).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com