
袋中共有10个大小相同的编号为1,2,3的球,其中1号球有1个,2号球有m个,3号球有n个.从袋中依次摸出2个球,已知在第一次摸出3号球的前提下,再摸出一个2号球的概率是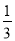 .
.
(1)求m,n的值;
(2)从袋中任意摸出2个球,设得到小球的编号数之和为ξ,求随机变量ξ的分布列.
 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-1函数的概念、定义域和值域(解析版) 题型:选择题
设函数f(x)= ,则不等式f(x)>f(1)的解集是( )
,则不等式f(x)>f(1)的解集是( )
A.(-3,1)∪(3,+∞) B.(-3,1)∪(2,+∞)
C.(-1,1)∪(3,+∞) D.(-∞,-3)∪(1,3)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:解答题
已知函数f(x)=x3-4x2+5x-4.
(1)求曲线f(x)在点(2,f(2))处的切线方程;
(2)求经过点A(2,-2)的曲线f(x)的切线方程.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-8n次独立重复实验与二项分布(解析版) 题型:填空题
在国庆期间,甲去北京旅游的概率为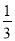 ,乙、丙去北京旅游的概率分别为
,乙、丙去北京旅游的概率分别为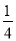 、
、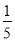 .假定三人的行动相互之间没有影响,那么这段时间内至少有一人去北京旅游的概率________.
.假定三人的行动相互之间没有影响,那么这段时间内至少有一人去北京旅游的概率________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:解答题
乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.
(1)求甲以4比1获胜的概率;
(2)求乙获胜且比赛局数多于5局的概率;
(3)求比赛局数的分布列.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:选择题
一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了ξ次球,则P(ξ=12)=( )
A.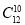 (
(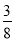 )10(
)10(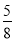 )2 B.
)2 B. (
(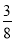 )9(
)9(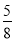 )2×
)2×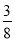
C.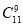 (
(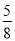 )9(
)9(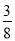 )2 D.
)2 D.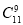 (
(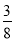 )9(
)9(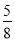 )2
)2
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-6几何概型(解析版) 题型:选择题
如图,矩形OABC内的阴影部分由曲线f(x)=sinx(x∈(0,π))及直线x=a(a∈(0,π))与x轴围成,向矩形OABC内随机投掷一点,若落在阴影部分的概率为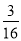 ,则a的值为( )
,则a的值为( )
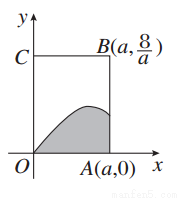
A.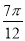 B.
B.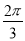 C.
C.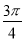 D.
D.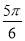
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-5古典概型(解析版) 题型:解答题
一个袋中有4个大小相同的小球,其中红球1个,白球2个,黑球1个,现从袋中有放回地取球,每次随机取1个.
(1)求连续取两次都是白球的概率;
(2)若取1个红球记2分,取1个白球记1分,取1个黑球记0分,求连续取两次的分数之和为2的概率.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-3二项式定理(解析版) 题型:选择题
在( +
+ )24的展开式中,x的幂指数是整数的项共有( )
)24的展开式中,x的幂指数是整数的项共有( )
A.3项 B.4项 C.5项 D.6项
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com