
已知函数f(x)=x3-4x2+5x-4.
(1)求曲线f(x)在点(2,f(2))处的切线方程;
(2)求经过点A(2,-2)的曲线f(x)的切线方程.
(1)x-y-4=0
(2)x-y-4=0或y+2=0
【解析】【解析】
(1)∵f′(x)=3x2-8x+5,
∴f′(2)=1,又f(2)=-2,
∴曲线f(x)在点(2,f(2))处的切线方程为y-(-2)=x-2,即x-y-4=0.
(2)设切点坐标为(x0,x03-4x02+5x0-4),
∵f′(x0)=3x02-8x0+5,
∴切线方程为y-(-2)=(3x02-8x0+5)(x-2),
又切线过点(x0,x03-4x02+5x0-4),
∴x03-4x02+5x0-2=(3x02-8x0+5)(x0-2),
整理得(x0-2)2(x0-1)=0,解得x0=2或x0=1,
∴经过A(2,-2)的曲线f(x)的切线方程为x-y-4=0或y+2=0.


科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-3函数的奇偶性与周期性(解析版) 题型:选择题
定义在R上的偶函数f(x)在[0,+∞)上是增函数,且f(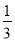 )=0,则不等式f(
)=0,则不等式f(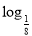 x)>0的解集是( )
x)>0的解集是( )
A.(0, ) B.(2,+∞)
) B.(2,+∞)
C.(0,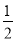 )∪(2,+∞) D.(
)∪(2,+∞) D.(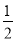 ,1)∪(2,+∞)
,1)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-12导数的应用二(解析版) 题型:填空题
已知函数f(x)=(x2-3x+3)ex,设t>-2,函数f(x)在[-2,t]上为单调函数时,t的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-11导数的应用一(解析版) 题型:选择题
函数f(x)的定义域是R,f(0)=2,对任意x∈R,f(x)+f′(x)>1,则不等式ex·f(x)>ex+1的解集为( )
A.{x|x>0}
B.{x|x<0}
C.{x|x<-1或x>1}
D.{x|x<-1或0<x<1}
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:填空题
已知函数y=f(x)的导函数为f′(x)=5+cosx,且f(0)=0,如果f(1-x)+f(1-x2)<0,则实数x的取值范围是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:2-10导数的概念及运算(解析版) 题型:选择题
已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)<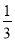 ,则f(x)<
,则f(x)<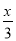 +
+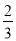 的解集为( )
的解集为( )
A.{x|-1<x<1} B.{x|x<-1}
C.{x|x<-1或x>1} D.{x|x>1}
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-8n次独立重复实验与二项分布(解析版) 题型:填空题
一盒中放有大小相同的10个小球,其中8个黑球、2个红球,现甲、乙二人先后各自从盒子中无放回地任意抽取2个小球,已知甲取到了2个黑球,则乙也取到2个黑球的概率是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-7离散型随机变量及分布列(解析版) 题型:解答题
袋中共有10个大小相同的编号为1,2,3的球,其中1号球有1个,2号球有m个,3号球有n个.从袋中依次摸出2个球,已知在第一次摸出3号球的前提下,再摸出一个2号球的概率是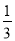 .
.
(1)求m,n的值;
(2)从袋中任意摸出2个球,设得到小球的编号数之和为ξ,求随机变量ξ的分布列.
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-4随机事件的概率(解析版) 题型:解答题
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示.
一次 购物量 | 1至 4件 | 5至 8件 | 9至 12件 | 13至 16件 | 17件及 以上 |
顾客数(人) | x | 30 | 25 | y | 10 |
结算时间 (分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
已知这100位顾客中一次购物量超过8件的顾客占55%.
(1)确定x,y的值,并估计顾客一次购物的结算时间的平均值;
(2)求一位顾客一次购物的结算时间不超过2分钟的概率.(将频率视为概率)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com