练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

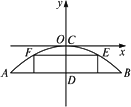
    一辆卡车高3 m，宽1.6 m，欲通过断面为抛物线形的隧道，如图所示，已知拱口宽AB恰好是拱高CD的4倍．若拱宽为a m，求能使卡车通过的a的最小整数值．

    答案：
    解析：

    　　解：以拱顶为原点，拱高所在直线为y轴，建立直角坐标系，

    　　设抛物线方程为x2＝－2py(p＞0)，则B()，

    　　由点B在抛物线上得＝－2p×()，

    　　∴p＝．故抛物线方程为x2＝－ay．

    　　将点E(0.8，y)代入抛物线方程得y＝．

    　　∴点E到拱底AB的距离为＞3．

    　　解得a＞12.21．

    　　∵a为整数．故a的最小整数值为13．


    提示：

    要求拱宽a的最小值需首先建立适当的坐标系，写出抛物线方程，然后利用方程求解．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：导学大课堂选修数学1-1苏教版 苏教版 题型：044

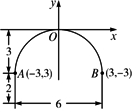
    一条隧道的横断面由抛物线弧及一个矩形的三边围成，尺寸如右图所示(单位：m)，一辆卡车空车时能通过此遂道，现载一集装箱，箱宽3 m，车与箱共高4.5 m，此车能否通过隧道？并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一条隧道的横断面由抛物线弧及一个矩形的三边围成，尺寸如图所示(单位：m)，一辆卡车空车时能通过此遂道，现载一集装箱，箱宽3 m，车与箱共高4.5 m，此车能否通过隧道？并说明理由.

    查看答案和解析>>

    同步练习册答案