
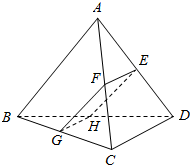
 如图,三棱锥A-BCD中,对棱AB与CD所成角为60°,且AB=CD=α,该三棱锥被一平面所截,截面为平行四边形EFGH.
如图,三棱锥A-BCD中,对棱AB与CD所成角为60°,且AB=CD=α,该三棱锥被一平面所截,截面为平行四边形EFGH.分析 (1)由已知得EF∥GH,从而EF∥平面BCD,进而EF∥CD,由此能证明CD∥平面EFGH.
(2)设$\frac{AE}{AD}$=x,则S=ax•(1-x)asin60°=$\frac{\sqrt{3}}{2}(1-x)x{a}^{2}$,由此能求出E为AD的中点时截面面积最大,并能求出面积的最大值.
(3)四边形EFGH的周长:C=2(EF+EH),由此能证明四边形EFGH的周长为定值.
解答 (1)证明:∵四边形EFGH为平行四边形,
∴EF∥GH,又GH?平面BCD,EF?平面BCD,
∴EF∥平面BCD,
∵平面ACD∩平面BCD=CD,EF?平面ACD,
∴EF∥CD,
∵EF?平面EFGH,CD?平面EFGH,
∴CD∥平面EFGH.
(2)解:设$\frac{AE}{AD}$=x,则EF=xCD=ax,EH=(1-x)AB=(1-x)a,∠FEH=60°,
∴S=ax•(1-x)asin60°=$\frac{\sqrt{3}}{2}(1-x)x{a}^{2}$,
当x=$\frac{1}{2}$时,${S}_{max}=\frac{\sqrt{3}}{8}{a}^{2}$,
∴E为AD的中点.
(3)证明:由(2)知,
四边形EFGH的周长:
C=2(EF+EH)=2[ax+a(1-x)]=2a为定值.
点评 本题考查线面平行的证明,考查截面面积最大时点的位置的确定,考查四边形EFGH的周长为定值的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{8}$) | B. | (-∞,0)∪(0,$\frac{1}{8}$) | C. | (0,$\frac{1}{8}$] | D. | ($\frac{1}{8}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,4} | B. | {3} | C. | a=0.42 | D. | b=30.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2<x+1 | B. | ?x∈R,x2≥x+1 | ||
| C. | ?x∈R,?y∈R,xy2=y2 | D. | ?x∈R,?y∈R,x>y2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com