
在等差数列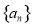 中,
中,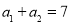 ,
,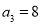 .令
.令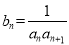 ,数列
,数列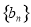 的前
的前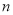 项和为
项和为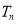 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列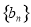 的前
的前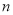 项和
项和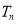 ;
;
(3)是否存在正整数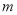 ,
,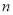 (
(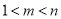 ),使得
),使得 ,
,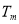 ,
,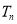 成等比数列?若存在,求出所有的
成等比数列?若存在,求出所有的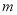 ,
,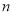 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)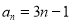 (2)
(2)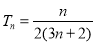 (3)存在满足条件的正整数
(3)存在满足条件的正整数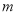 、
、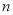 ,此时
,此时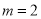 ,
,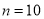
【解析】
试题分析:(1)因为数列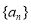 为等差数列,由
为等差数列,由 可求首项
可求首项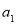 及公差
及公差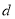 ,进而求得
,进而求得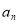 ;
;
(2)由(1)和题意易求得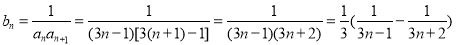 ,即可求得
,即可求得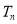 ;
;
(3)由(2)知,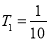 ,
,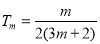 ,
,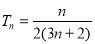 ,先假设存在正整数
,先假设存在正整数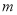 、
、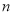
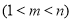 ,使得
,使得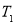 、
、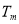 、
、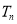 成等比数列,可得
成等比数列,可得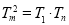 ,即
,即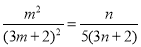 ,整理可得
,整理可得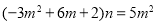 (*)当
(*)当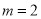 时,(*)式可化为
时,(*)式可化为 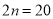 ,所以
,所以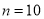 ;当
;当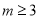 时,
时,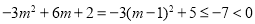 ,由
,由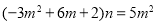 得
得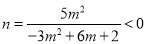 ,此时
,此时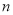 无正整数解,即可求得结果.
无正整数解,即可求得结果.
试题解析:(1)设数列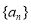 的公差为
的公差为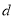 ,由
,由 得
得
解得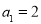 ,
,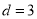 ∴
∴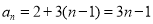
(2)∵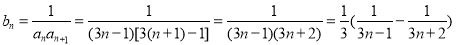
∴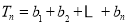
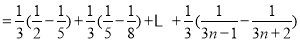
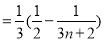

(3)由(2)知,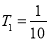 ,
,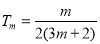 ,
,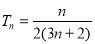
假设存在正整数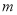 、
、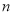
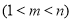 ,使得
,使得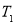 、
、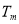 、
、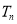 成等比数列,
成等比数列,
则 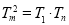 , 即
, 即 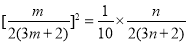
经化简,得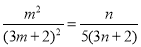
∴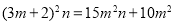
∴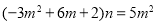 (*)
(*)
当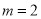 时,(*)式可化为
时,(*)式可化为 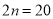 ,所以
,所以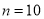
当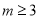 时,
时,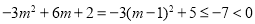
又∵ ,∴(*)式可化为
,∴(*)式可化为 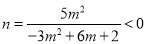 ,所以此时
,所以此时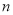 无正整数解.
无正整数解.
综上可知,存在满足条件的正整数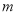 、
、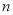 ,此时
,此时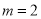 ,
,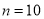 .
.
考点:等差数列的性质;裂项求和;等比数列的性质.


科目:高中数学 来源:2016届河南省实验学校高一下学期期末数学试卷2(解析版) 题型:选择题
将函数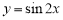 的图象沿x轴方向左平移
的图象沿x轴方向左平移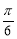 个单位, 则平移后的图象所对应函数的解析式是
个单位, 则平移后的图象所对应函数的解析式是
A.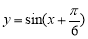 B.
B.
C. D.
D.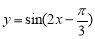
查看答案和解析>>
科目:高中数学 来源:2016届河南省高一下学期期末练习2数学试卷(解析版) 题型:选择题
200辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,则时速在[60,70)的汽车大约( )
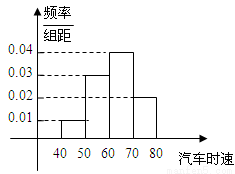
A.30辆 B.40辆 C.60辆 D.80辆
查看答案和解析>>
科目:高中数学 来源:2016届河南省高一下学期期末练习1数学试卷(解析版) 题型:选择题
某班5次数学测验中,甲、乙两同学的成绩如下:( )
甲:90 82 88 96 94; 乙:94 86 88 90 92
A.甲的平均成绩比乙好
B.甲的平均成绩比乙差
C.甲乙平均分相同,甲的成绩稳定性比乙好
D.甲乙平均分相同,乙的成绩稳定性比甲好
查看答案和解析>>
科目:高中数学 来源:2016届河南省高一下学期期末考试数学试卷(解析版) 题型:解答题
在△ABC中,角A,B,C的对边分别为a,b,c.角A,B,C成等差数列.
(1)求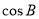 的值;
的值;
(2)边a,b,c成等比数列,求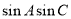 的值
的值
查看答案和解析>>
科目:高中数学 来源:2016届河南省周口市高一下学期期末考试数学试卷(解析版) 题型:填空题
如图,在平行四边形ABCD中,AP⊥BD,垂足为P,AP=3,点Q是△BCD内(包括边界)的动点,则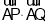 的取值范围是________.
的取值范围是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com