
分析 (Ⅰ)求出数列{an}的通项公式,再求数列{bn}的通项公式;
(Ⅱ)求出数列{cn}的通项,利用错位相减法求数列{cn}的前n项和Tn.
解答 解:(Ⅰ)Sn=3n2+8n,
∴n≥2时,an=Sn-Sn-1=6n+5,
n=1时,a1=S1=11,∴an=6n+5;
∵an=bn+bn+1,
∴an-1=bn-1+bn,
∴an-an-1=bn+1-bn-1.
∴2d=6,
∴d=3,
∵a1=b1+b2,
∴11=2b1+3,
∴b1=4,
∴bn=4+3(n-1)=3n+1;
(Ⅱ)cn=$\frac{({a}_{n}+1)^{n+1}}{({b}_{n}+2)^{n}}$=$\frac{(6n+6)^{n+1}}{(3n+3)^{n}}$=$\frac{(6n+6)^{n}(6n+6)}{(3n+3)^{n}}$=$\frac{{6}^{n}(n+1)^{n}(6n+6)}{{3}^{n}(n+1)^{n}}$=$\frac{{6}^{n}(6n+6)}{{3}^{n}}$=$\frac{(2×3)^{n}(6n+6)}{{3}^{n}}$=$\frac{(2×3)^{n}(6n+6)}{{3}^{n}}$=6(n+1)•2n,
∴Tn=6[2•2+3•22+…+(n+1)•2n]①,
∴2Tn=6[2•22+3•23+…+n•2n+(n+1)•2n+1]②,
①-②可得
-Tn=6[2•2+22+23+…+2n-(n+1)•2n+1]
=12+6×$\frac{2(1-{2}^{n})}{1-2}$-6(n+1)•2n+1
=(-6n)•2n+1=-3n•2n+2,
∴Tn=3n•2n+2.
点评 本题考查数列的通项与求和,着重考查等差数列的通项与错位相减法的运用,考查分析与运算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{10}$ | B. | $\frac{5}{8}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2sin(2x+$\frac{π}{4}$) | B. | y=2sin(2x+$\frac{π}{3}$) | C. | y=2sin(2x-$\frac{π}{4}$) | D. | y=2sin(2x-$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
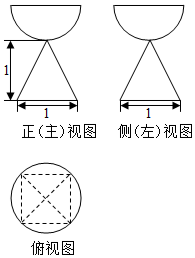 一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为( )
一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为( )| A. | $\frac{1}{3}$+$\frac{2}{3}$π | B. | $\frac{1}{3}$+$\frac{\sqrt{2}}{3}$π | C. | $\frac{1}{3}$+$\frac{\sqrt{2}}{6}$π | D. | 1+$\frac{\sqrt{2}}{6}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com