
已知函数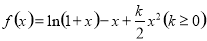 .
.
(1)当k=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)求f(x)的单调区间.
(1)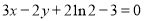 ;(2)当
;(2)当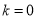 时,f(x)的单调递增区间是(-1,0),单调递减区间是(0,+∞);当
时,f(x)的单调递增区间是(-1,0),单调递减区间是(0,+∞);当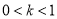 ,f(x)的单调递增区间是(-1,0)和(
,f(x)的单调递增区间是(-1,0)和(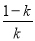 ,+∞),单调递减区间是(0,
,+∞),单调递减区间是(0,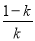 ).
).
当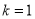 ,f(x)的单调递增区间是(-1,+∞);当
,f(x)的单调递增区间是(-1,+∞);当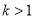 时,f(x)的单调递增区间是(-1,
时,f(x)的单调递增区间是(-1,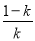 )和(0,+∞),单调递减区间是(
)和(0,+∞),单调递减区间是( ,0)
,0)
【解析】
试题分析:(1)利用导数的几何意义求曲线在点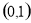 处的切线方程,注意这个点的切点,利用导数的几何意义求切线的斜率;(2)函数
处的切线方程,注意这个点的切点,利用导数的几何意义求切线的斜率;(2)函数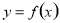 在某个区间内可导,则若
在某个区间内可导,则若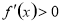 ,则
,则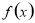 在这个区间内单调递增,若
在这个区间内单调递增,若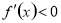 ,则
,则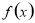 在这个区间内单调递减;(3)若可导函数
在这个区间内单调递减;(3)若可导函数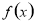 在指定的区间
在指定的区间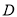 上单调递增(减),求参数问题,可转化为
上单调递增(减),求参数问题,可转化为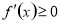
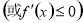 恒成立,从而构建不等式,要注意“=”是否可以取到.
恒成立,从而构建不等式,要注意“=”是否可以取到.
试题解析:解(1)当k=2时,f(x)=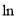 (1+x)-x+x2,f′(x)=
(1+x)-x+x2,f′(x)=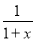 -1+2x.
-1+2x.
由于f(1)=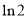 ,f′(1)=
,f′(1)=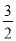 ,
,
所以曲线y=f(x)在点(1,f(1))处的切线方程为y-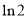 =
=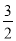 (x-1),即3x-2y+2ln 2-3=0.
(x-1),即3x-2y+2ln 2-3=0.
(2)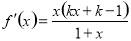 ,x∈(-1,+∞).
,x∈(-1,+∞).
当k=0时,f′(x)=-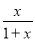 .所以,在区间(-1,0)上,f′(x)>0;在区间(0,+∞)上,f′(x)<0.
.所以,在区间(-1,0)上,f′(x)>0;在区间(0,+∞)上,f′(x)<0.
故f(x)的单调递增区间是(-1,0),单调递减区间是(0,+∞).
当0<k<1时,由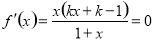 ,得x1=0,x2=
,得x1=0,x2=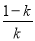 >0.
>0.
所以,在区间(-1,0)和(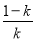 ,+∞)上,f′(x)>0;在区间(0,
,+∞)上,f′(x)>0;在区间(0,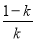 )上,f′(x)<0.
)上,f′(x)<0.
故f(x)的单调递增区间是(-1,0)和(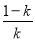 ,+∞),单调递减区间是(0,
,+∞),单调递减区间是(0,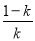 ).
).
当k=1时,f′(x)=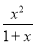 .故f(x)的单调递增区间是(-1,+∞).
.故f(x)的单调递增区间是(-1,+∞).
当k>1时,由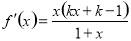 =0,得x1=
=0,得x1=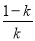 ∈(-1,0),x2=0.
∈(-1,0),x2=0.
所以,在区间(-1,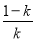 )和(0,+∞)上,f′(x)>0;在区间(
)和(0,+∞)上,f′(x)>0;在区间(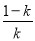 ,0)上,f′(x)<0.
,0)上,f′(x)<0.
故f(x)的单调递增区间是(-1,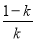 )和(0,+∞),单调递减区间是(
)和(0,+∞),单调递减区间是(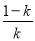 ,0).
,0).
考点:(1)求切线的斜率;(2)利用导数求函数的单调区间.


科目:高中数学 来源:2015届辽宁省鞍山市高二下学期期末考试理科数学试卷(解析版) 题型:解答题
设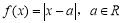 .
.
(1)当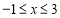 时,
时,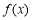 ≤3,求
≤3,求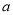 的取值范围;
的取值范围;
(2)若对任意的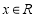 ,
,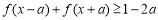 恒成立,求实数
恒成立,求实数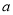 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省鞍山市高二下学期期末考试理科数学试卷(解析版) 题型:填空题
若多项式x2+x10=a0+a1(x+1)+ +a9(x+1)9+a10(x+1)10,则a9= .
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省鞍山市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
函数f(x)的定义域为开区间(a,b),导函数f ′(x)在(a,b)内的图象如下图所示,则函数f(x)在开区间(a,b)内有极大值点
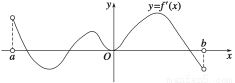
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2015届辽宁省分校高二新疆班下学期期末数学试卷(解析版) 题型:解答题
厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(1)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验,求至少有1件是合格品的概率;
(2)若厂家发给商家20件产品,其中有3件不合格.按合同规定该商家从中任取2件进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数ξ的分布列及数学期望E(ξ),并求该商家拒收这批产品的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com