(已知函数f(x)=k[(logax)2+(logxa)2]-(logax)3-(logxa)3,(其中a>1),g(x)=x2-2bx+4,设t=logax+logxa.
(Ⅰ)当x∈(1,a)∪(a,+∞)时,试将f(x)表示成t的函数h(t),并探究函数h(t)是否有极值;
(Ⅱ)当k=4时,若对任意的x1∈(1,+∞),存在x2∈[1,2],使f(x1)≤g(x2),试求实数b的取值范围..
解:(Ⅰ)∵(log
ax)
2+(log
xa)
2=(log
ax+log
xa)
2-2=t
2-2,
(log
ax)
3+(log
xa)
3=(log
ax+log
xa)[(log
ax+log
xa)
2-3]=t
3-3t,
∴h(t)=-t
3+kt
2+3t-2k,(t>2)∴h'(t)=-3t
2+2kt+3
设t
1,t
2是h'(t)=0的两根,则t
1t
2<0,
∴h'(t)=0在定义域内至多有一解,
欲使h(t)在定义域内有极值,只需h'(t)=-3t
2+2kt+3=0在(2,+∞)内有解,且h'(t)的值在根的左右两侧异号,∴h'(2)>0得

综上:当

时h(t)在定义域内有且仅有一个极值,当

时h(t)在定义域内无极值
(Ⅱ)∵对任意的x
1∈(1,+∞),存在x
2∈[1,2],使f(x
1)≤g(x
2)等价于x∈(1,+∞)时,f(x)
max≤g(x)
max,x∈[1,2],
又k=4时,h(t)=-t
3+4t
2+3t-8 (t≥2),
h'(t)=-3t
2+8t+3t∈(2,3)时,h'(t)>0,而t∈(3,+∞)时,h'(t)<0
∴h(t)
max=h(3)=10,

∴
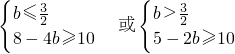
∴

分析:(I)根据完全平方公式和立方和关系进行化简变形,然后用t=log
ax+log
xa代入,即可将f(x)表示成t的函数h(t),欲使h(t)在定义域内有极值,只需h'(t)=0在(2,+∞)内有解,且h'(t)的值在根的左右两侧异号,h'(2)>0,即可求出所求;
(II)对任意的x
1∈(1,+∞),存在x
2∈[1,2],使f(x
1)≤g(x
2)等价于x∈(1,+∞)时,f(x)
max≤g(x)
max,x∈[1,2],然后利用导数研究最大值即可求出实数b的取值范围.
点评:本题主要考查了利用导数研究函数的极值,以及恒成立等有关知识,是一道综合题,有一定的难度,属于中档题.


 时h(t)在定义域内有且仅有一个极值,当
时h(t)在定义域内有且仅有一个极值,当 时h(t)在定义域内无极值
时h(t)在定义域内无极值
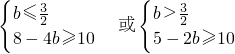 ∴
∴

