练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知0＜a＜1,判断函数f(x)=的奇偶性，并求出函数f(x)的周期.

    解:∵sin4-sin2

        =sin2(sin2-1)

        =-sin2cos2

        =-sin2x,

        f(x)==,

        得f(-x)===f(x).

        ∴f(x)是偶函数.

        又-sin2x=-·

        =-+cos2x,

        而cos2x的周期T==π,

        ∴f(x)的周期是π.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：上海市徐汇区2010届高三第二次模拟考试数学理科试题 题型：044

    已知函数f(x)＝

    (1)判断并证明y＝f(x)在x∈(0，＋∞)上的单调性；

    (2)若存在x0，使f(x0)＝x0，则称x0为函数f(x)的不动点，现已知该函数有且仅有一个不动点，求a的值，并求出不动点x0；

    (3)若f(x)＜2x在x∈(0，＋∞)上恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：广东省广州六校2012届高三第二次联考数学理科试题 题型：044

    已知二次函数．

    (1)判断命题：“对于任意的a∈R(R为实数集)，方程f(x)＝1必有实数根”的真假，并写出判断过程

    (2)若y＝f(x)在区间(－1，0)及内各有一个零点．求实数a的范围

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年潍坊市七模）  已知：（a＞1＞b＞0）．

    　　（1）求的定义域；

    　　（2）判断在其定义域内的单调性；

    　　（3）若在（1，＋∞）内恒为正，试比较a-b与1的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知0<a<1,在函数y= logax  (x≥1)的图象上有A、B、C三点，它们的横坐标分别是t、t+2、t+4；

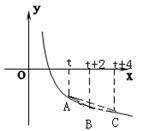    ①、记△ABC的面积为S，求出S=f(t)的表达式；并判断出S== f(t)的单调性；

    ②、求出S=f(t)的最大值。

    查看答案和解析>>

    同步练习册答案