
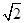 的直线
的直线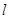 过椭圆
过椭圆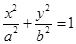
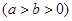 的右焦点,
的右焦点,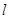 交椭圆于
交椭圆于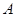 ,
,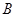 两
两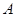 ,
,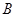 在椭圆长轴上的射影分别为
在椭圆长轴上的射影分别为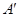 ,
,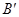 ,若
,若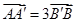 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( )A. | B. | C. | D. |
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源:不详 题型:单选题
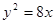 的准线与双曲线
的准线与双曲线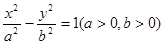 相交于A,B两点,双曲线的一条渐近线方程是
相交于A,B两点,双曲线的一条渐近线方程是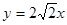 ,点F是抛物线的焦点,,且△
,点F是抛物线的焦点,,且△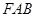 是直角三角形,则双曲线的标准方程是
是直角三角形,则双曲线的标准方程是A. | B.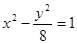 | C.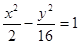 | D.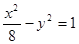 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
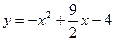 ,过原点O作抛物线C的切线
,过原点O作抛物线C的切线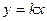 使切点P在第一象限,
使切点P在第一象限,查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 及点
及点 ,在
,在 上任取一点
上任取一点 ,线段
,线段 长度的最小值称为点
长度的最小值称为点 到线段
到线段 的距离,记作
的距离,记作 。
。 到线段
到线段 的距离
的距离 ;
; 是长为2的线段,求点集
是长为2的线段,求点集 所表示图形的面积;
所表示图形的面积; 距离相等的点的集合
距离相等的点的集合 ,其中
,其中 ,
, 是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。
是下列三组点中的一组。对于下列三组点只需选做一种,满分分别是①2分,②6分,③8分;若选择了多于一种的情形,则按照序号较小的解答计分。 。
。 。
。 。
。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com