练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图2-15,PA为⊙O的切线,A为切点,PBC是过O点的割线,PA =10,PB =5,∠BAC的平分线与BC和⊙O分别相交于D和E,

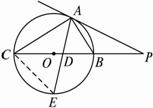
    图2-15

    求:(1)⊙O的半径;

    (2)sin∠BAP的值;

    (3)AD·AE的值.

    思路分析:(1)由PA2=PB·PC求出PC,从而求出半径.?

    (2)先把∠BAP转换到直角三角形中,利用∠BAP =∠ACB转换.?

    (3)直接求AD·AE较难,用相似三角形转换成其他线段之积.

    解:(1)∵PA2=PB·PC,PA =10,PB =5,?

    ∴PC=20,即BC=15.∴⊙O的半径为7.5.?

    (2)在△PBA和△PAC中,PA为切线,?

    ∴∠BAP=∠ACP.?

    又∵∠P =∠P,∴△PBA∽△PAC.?

    ∴=.∴=.?

    又∵AB为直径,∴∠BAC =90°.?

    设AB =x,则CA =2x,∴.?

    ∴sin∠ACB = = =.?

    又∵∠ACB =∠BAP,∴sin∠BAP =.?

    (3)连结CE,易证得△ACE∽△ADB,?

    ∴=,?

    即AD·AE =AB·AC.?

    由(2)得=,?

    ∵BC =15,∴AB =×15 =.?

    ∴AC =2AB =.?

    ∴AD·AE =×=90.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图2-4-15,PA、PB是⊙O的两条切线,A、B为切点,C是上一点,已知⊙O的半径为r,PO =2r,设∠PAC+∠PBC =α,∠APB =β,则α与β的大小关系为(　　)

    A.α＞β                  B.α=β                C.α＜β                         D.不能确定

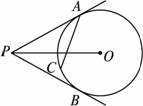
    图2-4-15

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图2-6,已知P是直径AB延长线上的一点,割线PCD交⊙O于C、D两点,弦DF⊥AB于点H,CF交AB于点E.

    (1)求证:PA·PB=PO·PE;

    (2)若DE⊥CF,∠P=15°,⊙O的半径为2,求CF的长.

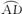
    图2-6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

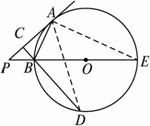
    如图2-5-19,已知PA为⊙O的切线,PO交⊙O于点B,BC⊥PA于点C,交⊙O于点D,

    图2-5-19

    (1)求证:AB2=PB·BD.

    (2)若PA =15,PB =5,求BD的长.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

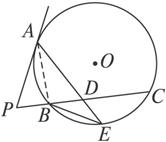
    如图2-5-15，PA切⊙O于A，割线PBC交⊙O于B、C，D为PC的中点，连结AD并延长交⊙O于E，已知BE2=DE·EA.

    图2-5-15

    求证：（1）PA=PD;

    （2）BP2=AD·DE.

    查看答案和解析>>

    同步练习册答案