
【题目】已知直线 ![]() ,若圆上恰好存在两个点
,若圆上恰好存在两个点 ![]() ,
,![]() ,他们到直线
,他们到直线 ![]() 的距离为
的距离为 ![]() ,则称该圆为“完美型”圆.则下列圆中是“完美型”圆的是
,则称该圆为“完美型”圆.则下列圆中是“完美型”圆的是 ![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】D
【解析】
根据题意,算出到直线l距离等于1的两条平行线方程为3x+4y﹣7=0或3x+4y﹣17=0,当圆与这两条直线共有2个公共点时满足该圆为“完美型”圆.由此对A、B、C、D各项中的圆分别加以判断,可得本题答案.
解:设直线l':3x+4y+m=0,l'与l的距离等于1则![]() ,解之得m=﹣7或﹣17,即l'的方程为3x+4y﹣7=0或3x+4y﹣17=0,可得当圆与3x+4y﹣7=0、3x+4y﹣17=0恰好有2个公共点时,满足该圆为“完美型”圆.
,解之得m=﹣7或﹣17,即l'的方程为3x+4y﹣7=0或3x+4y﹣17=0,可得当圆与3x+4y﹣7=0、3x+4y﹣17=0恰好有2个公共点时,满足该圆为“完美型”圆.
对于A,因为原点到直线l'的距离d=![]() 或
或![]() ,两条直线都与x2+y2=1相离,故x2+y2=1上不存在点,使点到直线l:3x+4y﹣12=0的距离为1,故A不符合题意.
,两条直线都与x2+y2=1相离,故x2+y2=1上不存在点,使点到直线l:3x+4y﹣12=0的距离为1,故A不符合题意.
对于B,因为原点到直线l'的距离d=![]() 或
或![]() ,两条直线都与x2+y2=16相交,故x2+y2=16上不存在4个点,使点到直线l:3x+4y﹣12=0的距离为1,故B不符合题意.
,两条直线都与x2+y2=16相交,故x2+y2=16上不存在4个点,使点到直线l:3x+4y﹣12=0的距离为1,故B不符合题意.
对于C,因为点(4,4)到直线l'的距离d=![]() 或
或![]() ,两条直线都与(x﹣4)2+(y﹣4)2=4相离,故(x﹣4)2+(y﹣4)2=4上不存在点,使点到直线l:3x+4y﹣12=0的距离为1,故C不符合题意.
,两条直线都与(x﹣4)2+(y﹣4)2=4相离,故(x﹣4)2+(y﹣4)2=4上不存在点,使点到直线l:3x+4y﹣12=0的距离为1,故C不符合题意.
对于D,因为点(4,4)到直线l'的距离d=![]() 或
或![]() ,所以两条直线中3x+4y﹣7=0与(x﹣4)2+(y﹣4)2=16相离,而3x+4y﹣17=0(x﹣4)2+(y﹣4)2=16相交,故(x﹣4)2+(y﹣4)2=16上恰好存在两个点P、Q,使点到直线l:3x+4y﹣12=0的距离为1,故D符合题意.
,所以两条直线中3x+4y﹣7=0与(x﹣4)2+(y﹣4)2=16相离,而3x+4y﹣17=0(x﹣4)2+(y﹣4)2=16相交,故(x﹣4)2+(y﹣4)2=16上恰好存在两个点P、Q,使点到直线l:3x+4y﹣12=0的距离为1,故D符合题意.
故选:D.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,且被
,且被![]() 轴所截得的弦长为
轴所截得的弦长为![]() ,圆心
,圆心![]() 在第一象限.
在第一象限.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() ,当△
,当△![]() 的面积最小时,求切线
的面积最小时,求切线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三一班举办消防安全知识竞赛,分别选出3名男生和3名女生组成男队和女队,每人一道必答题,答对则为本队得10分,答错与不答都得0分,已知男队每人答对的概率依次为 ![]() ,
, ![]() ,
, ![]() ,女队每人答对的概率都是
,女队每人答对的概率都是 ![]() ,设每人回答正确与否相互之间没有影响,用X表示男队的总得分.
,设每人回答正确与否相互之间没有影响,用X表示男队的总得分.
(I) 求X的分布列及其数学期望E(X);
(Ⅱ)求在男队和女队得分之和为50的条件下,男队比女队得分高的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC内角A,B,C的对边分别是a,b,c,且满足a( ![]() sinC+cosC)=b+c.
sinC+cosC)=b+c.
(I) 求角A的大小;
(Ⅱ)已知函数f(x)=sin(ωx+A)的最小正周期为π,求f(x)的减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次数学竞赛中,30名参赛学生的成绩(百分制)的茎叶图如图所示:若将参赛学生按成绩由高到低编为1﹣30号,再用系统抽样法从中抽取6人,则其中抽取的成绩在[77,90]内的学生人数为( ) 
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
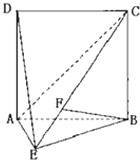
【题目】如图,直二面角![]() 中,四边形ABCD是边长为2的正方形,
中,四边形ABCD是边长为2的正方形,![]() ,F为CE上的点,且
,F为CE上的点,且![]() 平面ACE.
平面ACE.
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面BCE;
平面BCE;
![]() Ⅱ
Ⅱ![]() 求二面角
求二面角![]() 的余弦值;
的余弦值;
![]() Ⅲ
Ⅲ![]() 求点D到平面ACE的距离.
求点D到平面ACE的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com