

(1)求异面直线SC和AB的距离;
(2)求异面直线SA和EF所成的角.
解析:(1)连结SF、CF,?
∵△SAB、△CAB是正三角形,∴SF=CF=![]() a,且SF虯B,CF⊥AB.?
a,且SF虯B,CF⊥AB.?
又SF∩CF=F,∴AB⊥面SFC.?
∴AB⊥EF于F.?
又SF=CF,∴△FSC是等腰三角形.?
又E是SC中点,∴FE⊥SC于E.?
∴EF是SC与AB的公垂线段.?
在Rt△SEF中,SF=![]() a,SE=
a,SE=![]() a,?
a,?
∴由勾股定理可知EF=![]() .?
.?
因此,异面直线SC与AB的距离为![]() .?
.?
(2)取AC中点M,连结EM、FM.?
∵E、F、M分别为SC、AB、CA中点,?
∴EM∥SA,FM∥CB,?
且EM=![]() SA,FM=
SA,FM=![]() CB.?
CB.?
∴EM=FM=12a.?
∴∠MEF是SA与EF所成的角或其补角.?
∵EM=FM=![]() a,EF=
a,EF=![]() a,?
a,?
∴EF2=FM2+EM2,即FM⊥EM.?
∴△EMF是等腰直角三角形.?
∴∠MFE=45°,即SA与EF所成的角是45°.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
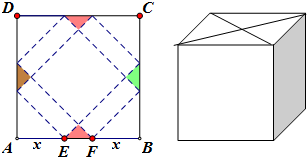 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省威海四中高二(下)期中数学试卷(文科)(解析版) 题型:解答题
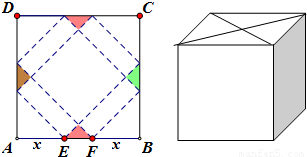 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).查看答案和解析>>
科目:高中数学 来源:2011-2012年学广东省梅州市东山中学高三(上)期中数学试卷(理科)(解析版) 题型:解答题
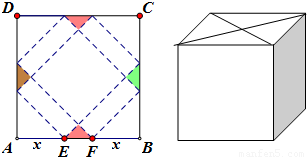 请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).
请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得A,B,C,D四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上,是被切去的等腰直角三角形斜边的两个端点,设AE=FB=x(cm).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com