
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源:不详 题型:解答题
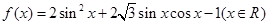 .
.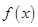 的图像是由函数
的图像是由函数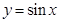 的图像经过怎样的变换得到的;
的图像经过怎样的变换得到的;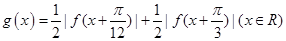 ,试判断函数
,试判断函数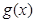 的奇偶性,并用反证法证明函数
的奇偶性,并用反证法证明函数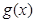 的最小正周期是
的最小正周期是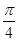 ;
;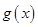 的单调区间和值域.
的单调区间和值域.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 方案 | 类别 | 基本费用 | 超时费用 |
| 甲 | 包月制(不限时) | 100元 | 无 |
| 乙 | 有限包月制(限60小时) | 60元 | 3元/小时(无上限) |
| 丙 | 有限包月制(限30小时) | 40元 | 3元/小时(无上限) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com