
分析 (1)根据函数单调性的定义进行证明即可,
(2)根据函数的性质利用作差法进行判断即可,
(3)根据 函数定义域和值域的关系建立方程,进行求解即可.
解答 解:(1)∵f($\frac{1}{x}$)=$\frac{1}{x}$+$\frac{1}{\frac{1}{x}}$=x+$\frac{1}{x}$=f(x),∴函数f(x)具有性质M.
任取x1、x2且x1<x2,
则f(x1)-f(x2)=(x1+$\frac{1}{{x}_{1}}$)-(x2+$\frac{1}{{x}_{2}}$)=(x1-x2)+($\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$)=(x1-x2)•$\frac{{x}_{1}{x}_{2}-1}{{x}_{1}{x}_{2}}$,
若x1、x2∈(0,1),
则0<x1x2<1,x1x2>0,x1-x2<0,
∴f(x1)-f(x2)>0,
∴f(x1)>f(x2),
∴f(x)在(0,1)上是减函数.
若x1、x2∈(1,+∞),
则x1x2>1,x1-x2<0,
∴f(x1)-f(x2)<0,
∴f(x1)<f(x2),
∴f(x)在(1,+∞)上是增函数.
(2)∵$g(\frac{1}{x})=|ln\frac{1}{x}|=|-lnx|=|lnx|=g(x)$,∴g(x)具有性质M (4分)
由|lnx|=t得,lnx=-t或lnx=t,x=e-t或x=et,
∵t>0,∴e-t<et,
∴${x_B}={e^{-t}},{x_c}={e^t}$,
∴$|AB|=\sqrt{{{(1-{x_B})}^2}+{t^2}}=\sqrt{{{(1-{e^{-t}})}^2}+{t^2}}$,∴$|AC|=\sqrt{{{(1-{x_c})}^2}+{t^2}}=\sqrt{{{(1-{e^t})}^2}+{t^2}}$,
∴|AB|2-|AC|2=(1-e-t)2-(1-et)2=[2-(e-t+et)](et-e-t)
由(1)知,$f(x)=x+\frac{1}{x}$在x∈(0,+∞)上的最小值为1(其中x=1时)
而$0<{e^{-t}}=\frac{1}{e^t}<1<{e^t}$,故2-(e-t+et)<0,et-e-t>0,
|AB|<|AC|(7分)
(3)∵h(1)=0,m,n,k均为正数,
∴0<m<n<1或1<m<n(8分)
当0<m<n<1时,0<x<1,$h(x)=|x-\frac{1}{x}|$=$\frac{1}{x}-x$是减函数,
值域为(h(n),h(m)),h(n)=km,h(m)=kn,
∴$\frac{h(n)}{h(m)}=\frac{m}{n}$,∴$\frac{{\frac{1}{n}-n}}{{\frac{1}{m}-m}}=\frac{m}{n}$,∴1-n2=1-m2
故不存在 (10分)
当1<m<n时,x>1,$h(x)=|x-\frac{1}{x}|$=$x-\frac{1}{x}$是增函数,
∴h(m)=km,h(n)=kn,∴$m-\frac{1}{m}=km,n-\frac{1}{n}=kn$,
∴(1-k)m2=1,(1-k)n2=1,${m^2}={n^2}=\frac{1}{1-k}$,不存在
综合得,若不存在正数m,n,k满足条件. (12分)
点评 本题主要考查函数与方程的应用,结合新定义,以及利用函数与方程的关系进行转化是解决本题的关键.综合性较强,难度较大.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥$\sqrt{3}$ | B. | m≤$\sqrt{3}$ | C. | m≤-$\sqrt{3}$ | D. | -$\sqrt{3}$≤m≤$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
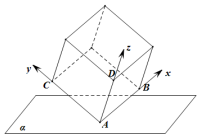 如图,棱长为3的正方体的顶点A在平面α上,三条棱AB、AC、AD都在平面α的同侧.若顶点B,C到平面α的距离分别为1,$\sqrt{2}$.建立如图所示的空间直角坐标系,设平面α的一个法向量为(x1,y1,z1),顶点D到平面α的距离为h.若x1=1,则y1+z1+h=$\sqrt{2}$+2$\sqrt{6}$.
如图,棱长为3的正方体的顶点A在平面α上,三条棱AB、AC、AD都在平面α的同侧.若顶点B,C到平面α的距离分别为1,$\sqrt{2}$.建立如图所示的空间直角坐标系,设平面α的一个法向量为(x1,y1,z1),顶点D到平面α的距离为h.若x1=1,则y1+z1+h=$\sqrt{2}$+2$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com