
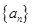 ,其前n项和
,其前n项和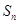 满足
满足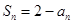 ;等差数列
;等差数列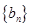 中
中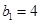 ,且
,且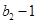 是
是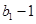 与
与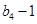 的等比中项
的等比中项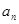 和
和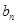 ,
,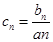 ,求
,求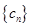 的前n项和
的前n项和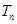 .
.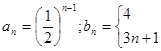
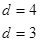 ;(2)
;(2)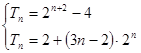
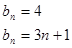 .
.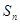 求
求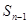 ,然后两式相减得出
,然后两式相减得出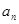 的递推形式,
的递推形式,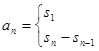
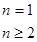 ,不要忘了验证
,不要忘了验证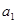 是否满足
是否满足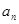 ,从而求出
,从而求出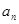 的通项公式,
的通项公式,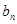 为等差数列,设
为等差数列,设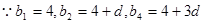 ,按照这三项成等比数列,可以通过已知建立方程求出
,按照这三项成等比数列,可以通过已知建立方程求出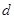 ,然后求出
,然后求出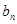 通项;(2)分类讨论思想,(1)问求出,
通项;(2)分类讨论思想,(1)问求出,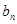 的通项公式有两个,所以
的通项公式有两个,所以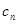 也是两个,其中
也是两个,其中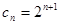 或
或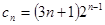 ,第一个通项公式按等比数列的前N项和求解,第二个按错位相减法,列出
,第一个通项公式按等比数列的前N项和求解,第二个按错位相减法,列出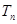 ,再列出q
,再列出q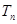 ,
,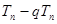 ,求出
,求出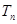 .运算量比较大.平时要加强训练.此题为中档题.
.运算量比较大.平时要加强训练.此题为中档题.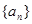 由题可知
由题可知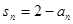 ①
①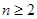 时,
时,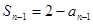 ②
②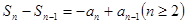 1分
1分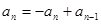 ,
,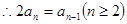
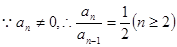 2分
2分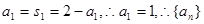 是以1为首项,以
是以1为首项,以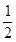 为公比的等比数列
为公比的等比数列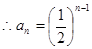 3分
3分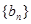 的公比为
的公比为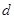 ,由题知
,由题知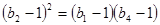 4分
4分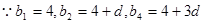
 ,解得
,解得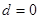 或
或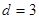
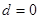 时,
时,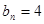 ;当
;当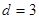 时,
时,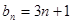 6分
6分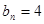 时,
时,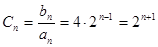
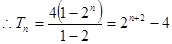 7分
7分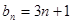 时,
时,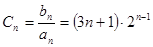
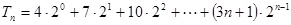 ③
③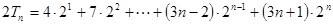 ④ 8分
④ 8分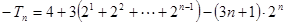
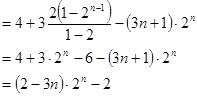
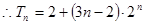 11分
11分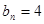 时,
时,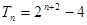 ;
;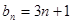 时,
时, 12分
12分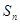 求
求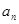 ;3.错位相减法求和.
;3.错位相减法求和.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com